题目内容
设α表示平面,a,b表示直线,给定下面四个命题:
①a∥α,a⊥b→b⊥α;
②a∥b,a⊥α→b⊥α;
③a⊥α,a⊥b→b∥α;
④a⊥α,b⊥α→a∥b.
其中正确的命题是 .(填序号)
①a∥α,a⊥b→b⊥α;
②a∥b,a⊥α→b⊥α;
③a⊥α,a⊥b→b∥α;
④a⊥α,b⊥α→a∥b.
其中正确的命题是
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:由线面平行的性质,可判断①;由线面垂直的性质:两条平行线中的一条垂直于一个平面,另一条也垂直于这个平面,即可判断②;由线面垂直的性质,即可判断③;由线面垂直的性质:同垂直于一个平面的两直线平行,即可判断④.
解答:
解:①若a∥α,a⊥b,则b∥α或b?α或b⊥α,故①错;
②若a∥b,a⊥α,则由线面垂直的性质:两条平行线中的一条垂直于一个平面,另一条也垂直于这个平面,
即b⊥α,故②正确;
③若a⊥α,a⊥b,则b∥α或b?α,故③错;
④若a⊥α,b⊥α,则由同垂直于一个平面的两直线平行,即a∥b,故④正确.
故答案为:②④.
②若a∥b,a⊥α,则由线面垂直的性质:两条平行线中的一条垂直于一个平面,另一条也垂直于这个平面,
即b⊥α,故②正确;
③若a⊥α,a⊥b,则b∥α或b?α,故③错;
④若a⊥α,b⊥α,则由同垂直于一个平面的两直线平行,即a∥b,故④正确.
故答案为:②④.
点评:本题主要考查直线与平面的位置关系,考查线面平行、垂直的判定和性质,是一道基础题.

练习册系列答案
相关题目
抛物线y2=-8x中,以(-1,1)为中点的弦所在的直线方程是( )
| A、x-4y-3=0 |
| B、x+4y+3=0 |
| C、4x+y-3=0 |
| D、4x+y+3=0 |
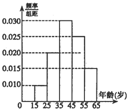 某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示:
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示: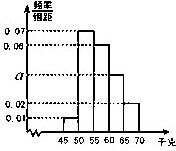 为了了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位为千克)全部介于45至70之间,将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70),得到如图所示的频率分布直方图,则a=
为了了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位为千克)全部介于45至70之间,将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70),得到如图所示的频率分布直方图,则a=