Question

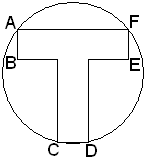某工厂接到一标识制作订单，标识如图所示，分为两部分，“T型”部分为宽为10cm 的两个矩形相接而成，圆面部分的圆周是A，C，D，F的外接圆．要求如下：①“T型”部分的面积不得小于800cm²；②两矩形的长均大于外接圆半径．为了节约成本，设计时应尽量减小圆面的面积．此工厂的设计师，凭直觉认为当“T型”部分的面积取800cm²且两矩形的长相等时，成本是最低的．你同意他的观点吗？试通过计算，说说你的理由．

Answer 1

考点：基本不等式在最值问题中的应用

专题：计算题,应用题,不等式的解法及应用

分析：设一个矩形长AF=x（dm），则另一矩形长为8-x（dm）．设圆半径为r（dm），则

r2- 1 4 x2

-1+

r2- 1 4

=8-x，化简整理，令9-x=t，得到2

r2- 1 4

=

5

4

（t+

16

t

）-

9

2

，再由基本不等式即可得到最小值，注意等号成立的条件．

解答： 解：设一个矩形长AF=x（dm），则另一矩形长为8-x（dm）．
设圆半径为r（dm），则

r2- 1 4 x2

-1+

r2- 1 4

=8-x，
r²-

1

4

x²=（9-x）²+r²-

1

4

-2（9-x）

r2- 1 4

，
即2（9-x）

r2- 1 4

=（9-x）²+

1

4

x²-

1

4

．
令9-x=t，得2t

r2- 1 4

=t²+

1

4

（9-t）²-

1

4

=

5

4

t²+20-

9

2

t，
得2

r2- 1 4

=

5

4

（t+

16

t

）-

9

2

≥

5

4

×2

t• 16 t

-

9

2

=

11

2

，
即r²≥

121

16

+

1

4

，
即有r≥

5 5

4

，
此时t=4即有x=5，y=3（单位：dm）．
则不同意他的观点．

点评：本题考查基本不等式在最值问题中的运用，根据题意得到等式，通过换元化简整理是解题的关键，考查运算能能力，属于中档题．