题目内容
已知数列{an}各项均为正数,其前n项和Sn满足2Sn=a
+an(n∈N*).
(1)证明:{an}为等差数列;
(2)令bn=
,记{bn}的前n项和为Tn,求证:Tn≤
.
2 n |
(1)证明:{an}为等差数列;
(2)令bn=
| lnan | ||
|
| 2n2-n-1 |
| 4(n+1) |
考点:数列与不等式的综合,等差关系的确定
专题:等差数列与等比数列
分析:(1)由已知得2an=an2-an-12+an-an-1,从而(an+an-1)(an-an-1-1)=0,由此能证明{an}是以1为首项1为公差的等差数列.(6分)
(2)由an=n,bn=
=
,得欲证Tn≤
,即证:Tn=
+
+
+…+
≤
,设f(x)=lnx-x+1,x>0,则f′(x)=
-1=
,由此利用导数性质能证明Tn≤
.
(2)由an=n,bn=
| lnan | ||
|
| lnn |
| n2 |
| 2n2-n-1 |
| 4(n+1) |
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln4 |
| 4 |
| lnn |
| n |
| 2n2-n-1 |
| 4(n+1) |
| 1 |
| x |
| 1-x |
| x |
| 2n2-n-1 |
| 4(n+1) |
解答:
(1)证明:∵2Sn=an2+an,①
∴2Sn-1=an-12+an-1(n≥2)②
①-②得2an=an2-an-12+an-an-1,
整理得(an+an-1)(an-an-1-1)=0,
∵an+an-1≠0,∴an-an-1=1(常数)
又4S1=4a1=a12+a1,
即a12-a1=0,解得a1=1,
∴{an}是以1为首项1为公差的等差数列.(6分)
(2)证明:由(1)知an=n,bn=
=
,
∴欲证Tn≤
,即证:Tn=
+
+
+…+
≤
,
设f(x)=lnx-x+1,x>0,
则f′(x)=
-1=
,
当x∈(0,1),f′(x)>0,f(x)为单调递增函数,
当x∈(1,+∞),f′(x)<0,f(x)单调递减函数;
∴在x=1处f(x)取得极大值,也取得最大值.
∴f(x)≤f(1)=0,即lnx-x+1≤0,
∴lnx≤x-1,∴
≤
=1-
,
n∈N*,n≥2时,令x=n2,得
≤1-
,
∴
≤
(1-
),
∴
+
+…+
≤
(1-
+1-
+…+1-
)
=
[(n-1)-(
+
+…+
)]
<
[(n-1)-(
+
+…+
]
=
[n-1-(
-
+
-
+…+
-
)]
=
[n-1-(
-
)]
=
,
∴当n=1,有Tn=
=0.
故Tn≤
.(13分)
∴2Sn-1=an-12+an-1(n≥2)②
①-②得2an=an2-an-12+an-an-1,
整理得(an+an-1)(an-an-1-1)=0,
∵an+an-1≠0,∴an-an-1=1(常数)
又4S1=4a1=a12+a1,
即a12-a1=0,解得a1=1,
∴{an}是以1为首项1为公差的等差数列.(6分)
(2)证明:由(1)知an=n,bn=
| lnan | ||
|
| lnn |
| n2 |
∴欲证Tn≤
| 2n2-n-1 |
| 4(n+1) |
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln4 |
| 4 |
| lnn |
| n |
| 2n2-n-1 |
| 4(n+1) |
设f(x)=lnx-x+1,x>0,
则f′(x)=
| 1 |
| x |
| 1-x |
| x |
当x∈(0,1),f′(x)>0,f(x)为单调递增函数,
当x∈(1,+∞),f′(x)<0,f(x)单调递减函数;
∴在x=1处f(x)取得极大值,也取得最大值.
∴f(x)≤f(1)=0,即lnx-x+1≤0,
∴lnx≤x-1,∴
| lnx |
| x |
| x-1 |
| x |
| 1 |
| x |
n∈N*,n≥2时,令x=n2,得
| lnn2 |
| n2 |
| 1 |
| n2 |
∴
| lnn |
| n2 |
| 1 |
| 2 |
| 1 |
| n2 |
∴
| ln2 |
| 22 |
| ln3 |
| 32 |
| lnn |
| n2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
<
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
=
| 2n2-n-1 |
| 4(n+1) |
∴当n=1,有Tn=
| 2n2-n-1 |
| 4(n+1) |
故Tn≤
| 2n2-n-1 |
| 4(n+1) |
点评:本题考查等差数列的证明,考查不等式的证明,解题时要认真审题,注意构造法和导数性质的合理运用.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
设D为不等式组
表示的平面区域,点B(a,b)为坐标平面xOy内一点,若对于区域D内的任一点A(x,y),都有
•
≤1成立,则a+b的最大值等于( )
|
| OA |
| OB |
| A、2 | B、1 | C、0 | D、3 |
函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是( )
| A、(-∞,-1] |
| B、(-∞,-1) |
| C、[-1,+∞) |
| D、(-1,+∞) |
平面向量
,
满足
=2
如果
=(1,1),那么
等于( )
| a |
| b |
| b |
| a |
| a |
| b |
| A、-(2,2) |
| B、(-2,-2) |
| C、(2,-2) |
| D、(2,2) |
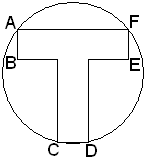 某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.
某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.