题目内容
已知函数y=Asin(ωt+φ)(其中A>0,ω>0,|φ|<
)的图象如图1所示,它刻画了质点P做匀速圆周运动(如图2)时,质点相对水平直线l的位置值y(|y|是质点与直线l的距离(米),质点在直线l上方时,y为正,反之y为负)随时间t(秒)的变化过程.则

(1)质点P运动的圆形轨道的半径为 米;
(2)质点P旋转一圈所需的时间T= 秒;
(3)函数f(t)的解析式为: ;
(4)图2中,质点P首次出现在直线l上的时刻t= 秒.
| π |
| 2 |

(1)质点P运动的圆形轨道的半径为
(2)质点P旋转一圈所需的时间T=
(3)函数f(t)的解析式为:
(4)图2中,质点P首次出现在直线l上的时刻t=
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由图1可得A=2,可得质点P运动的圆形轨道的半径为2.
(2)质点P旋转一圈所需的时间T,即函数y=Asin(ωt+φ)的周期.把点(0,-1)代入函数的解析式求得φ;再把点(
,2)代入函数的解析式求得ω,可得函数的周期.
(3)由(2)中的φ、ω的值,可得f(t)的解析式.
(4)令f(t)=2sin(πt-
)=0,求得πt-
=kπ,k∈z,求得t的最小正值,即为所求.
(2)质点P旋转一圈所需的时间T,即函数y=Asin(ωt+φ)的周期.把点(0,-1)代入函数的解析式求得φ;再把点(
| 2 |
| 3 |
(3)由(2)中的φ、ω的值,可得f(t)的解析式.
(4)令f(t)=2sin(πt-
| π |
| 6 |
| π |
| 6 |
解答:
解:(1)由图1可得A=2,故质点P运动的圆形轨道的半径为2,故答案为:2.
(2)质点P旋转一圈所需的时间T,即函数y=Asin(ωt+φ)的周期,
把点(0,-1)代入函数的解析式可得2sinφ=-1,可得sinφ=-
,再结合|φ|<
,可得φ=-
.
再把点(
,2)代入函数的解析式可得 2sin(ω•
-
)=2,即sin(ω•
-
)=1,(ω•
-
)=
,求得ω=π,
故函数的周期为
=2,
故答案为:2.
(3)由(2)可得f(t)=2sin(πt-
),
故答案为:f(t)=2sin(πt-
).
(4)令f(t)=2sin(πt-
)=0,求得πt-
=kπ,k∈z,可得t的最小正值为
,
故答案为:
.
(2)质点P旋转一圈所需的时间T,即函数y=Asin(ωt+φ)的周期,
把点(0,-1)代入函数的解析式可得2sinφ=-1,可得sinφ=-
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
再把点(
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |
| π |
| 2 |
故函数的周期为
| 2π |
| π |
故答案为:2.
(3)由(2)可得f(t)=2sin(πt-
| π |
| 6 |
故答案为:f(t)=2sin(πt-
| π |
| 6 |
(4)令f(t)=2sin(πt-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象和性质应用,体现了转化的数学思想,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
双曲线x2-2y2=1的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知椭圆
+
=1上一点P到两焦点距离的乘积为m,当m取得最大值时,点P的坐标是( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、(3,0)和(-3,0) |
| B、(0,3)和(0,-3) |
| C、(4,0)和(-4,0) |
| D、(0,4)和(0,-4) |

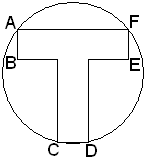 某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.
某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由. 如图所示的程序框图中,该程序运行后输出的结果为
如图所示的程序框图中,该程序运行后输出的结果为