题目内容
观察以下等式:
C51+C35=23-2,C91+C95+C99=27+23
C131+C135+C139+C1311=211-25
C171+C175+C179+1713+C1717=215+27
由此推测:C20131+C20135+C2013∅+…+C20132013= .
C51+C35=23-2,C91+C95+C99=27+23
C131+C135+C139+C1311=211-25
C171+C175+C179+1713+C1717=215+27
由此推测:C20131+C20135+C2013∅+…+C20132013=
考点:归纳推理
专题:推理和证明
分析:通过观察归纳出:第n个等式的右边由二项构成,第一项为:24n-1,第二项为(-1)n•22n-1,进而根据4n+1=2013,n=503,得到答案.
解答:
解:由已知中等式:
C51+C35=23-2,C91+C95+C99=27+23,
C131+C135+C139+C1311=211-25,
C171+C175+C179+1713+C1717=215+27,
由此推测:第n个等式的右边由二项构成,第一项为:24n-1,第二项为(-1)n•22n-1,
由4n+1=2013,n=503,可得4n-1=2011,2n-1=1005
C20131+C20135+C2013∅+…+C20132013=22011-21005.
故答案为:22011-21005.
C51+C35=23-2,C91+C95+C99=27+23,
C131+C135+C139+C1311=211-25,
C171+C175+C179+1713+C1717=215+27,
由此推测:第n个等式的右边由二项构成,第一项为:24n-1,第二项为(-1)n•22n-1,
由4n+1=2013,n=503,可得4n-1=2011,2n-1=1005
C20131+C20135+C2013∅+…+C20132013=22011-21005.
故答案为:22011-21005.
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设D为不等式组
表示的平面区域,点B(a,b)为坐标平面xOy内一点,若对于区域D内的任一点A(x,y),都有
•
≤1成立,则a+b的最大值等于( )
|
| OA |
| OB |
| A、2 | B、1 | C、0 | D、3 |
已知椭圆
+
=1上一点P到两焦点距离的乘积为m,当m取得最大值时,点P的坐标是( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、(3,0)和(-3,0) |
| B、(0,3)和(0,-3) |
| C、(4,0)和(-4,0) |
| D、(0,4)和(0,-4) |


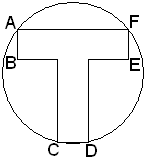 某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.
某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.