题目内容
数列{bn}的前n项和为Sn,Sn=
n(n+1)b1,b7=21,数列{an}满足a1b1+a2b2+…+anbn=n(n+1)(2n+1).
(1)求an;
(2)Tn=a1-a2+a3-a4+…+(-1)n+1•an,求Tn;
(3)求证:
+
+…+
<
.
| 1 |
| 2 |
(1)求an;
(2)Tn=a1-a2+a3-a4+…+(-1)n+1•an,求Tn;
(3)求证:
| 1 |
| a12 |
| 1 |
| a22 |
| 1 |
| an2 |
| 1 |
| 2 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(1)根据题意和公式bn=Sn-Sn-1(n≥2)求出bn,同样的方法求出anbn,再求出an并验证n=1时成立;
(2)把(1)求出的an代入Tn化简后,对n分奇数和偶数讨论,分别求出对应的式子,再分段表示出来;
(3)把(1)求出的an代入不等式的左边化简后,把分母缩小并进行裂项并逐项相消后,根据式子的特点和n的取值证明不等式成立.
(2)把(1)求出的an代入Tn化简后,对n分奇数和偶数讨论,分别求出对应的式子,再分段表示出来;
(3)把(1)求出的an代入不等式的左边化简后,把分母缩小并进行裂项并逐项相消后,根据式子的特点和n的取值证明不等式成立.
解答:
解:(1)由题意得,Sn=
n(n+1)b1,b7=21,
∴bn=Sn-Sn-1=
n(n+1)b1-
n(n-1)b1=nb1(n≥2),
∴{bn}为等差数列,
∵b7=7b1=21,∴b1=3,∴bn=3n,
由a1b1+a2b2+…+anbn=n(n+1)(2n+1)可得,
当n≥2时,a1b1+a2b2+…+an-1bn-1=(n-1)n(2n-1)
两个式子相减得,anbn=6n2(n≥2),
∴an=2n(n≥2),
由于a1b1=2×3=6,a1=2,
∴an=2n,
(2)由(1)得,an=2n,
Tn=a1-a2+a3-a4+…+(-1)n+1•an,
∴Tn=2-4+6-8+…+(-1)n+1•2n
=2[(1-2)+(3-4)+…+(-1)n+1•n]
当n为奇数时,Tn=2[(-1)×
+n]=n+1;
当n为偶数时,Tn=2[(-1)×
]=-n,
∴Tn=
,
(3)由(1)得,an=2n,
则
+
+…+
=
(
+
+…+
)
<
(1+
+
+…+
)
=[1+(1-
)+(
-
)+…+(
-
)]
=
(1+1-
)=
-
<
.
| 1 |
| 2 |
∴bn=Sn-Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
∴{bn}为等差数列,
∵b7=7b1=21,∴b1=3,∴bn=3n,
由a1b1+a2b2+…+anbn=n(n+1)(2n+1)可得,
当n≥2时,a1b1+a2b2+…+an-1bn-1=(n-1)n(2n-1)
两个式子相减得,anbn=6n2(n≥2),
∴an=2n(n≥2),
由于a1b1=2×3=6,a1=2,
∴an=2n,
(2)由(1)得,an=2n,
Tn=a1-a2+a3-a4+…+(-1)n+1•an,
∴Tn=2-4+6-8+…+(-1)n+1•2n
=2[(1-2)+(3-4)+…+(-1)n+1•n]
当n为奇数时,Tn=2[(-1)×
| n-1 |
| 2 |
当n为偶数时,Tn=2[(-1)×
| n |
| 2 |
∴Tn=
|
(3)由(1)得,an=2n,
则
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| n2 |
<
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)×n |
=[1+(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
=
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 4n |
| 1 |
| 2 |
点评:本题考查了等差数列的通项公式,数列前n项和公式与通项公式的关系,利用裂项相消法求数列的前n项和,考查了分类讨论思想,以及放缩法证明不等式成立问题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知
,
是夹角为60°的两个单位向量,则
=2
+
与
=-3
+2
的夹角的正弦值是( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若四点A(5,0),B(-1,0),C(a,2),D(3,-2)共圆,则正实数a=( )
| A、2 | B、3 | C、4 | D、5 |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.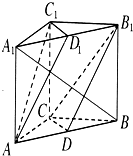 如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.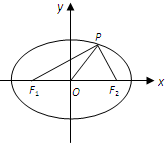 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆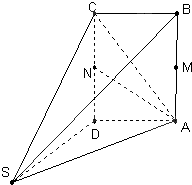 如图,多面体ABCDS中,四边形ABCD为矩形,SD⊥AD,SD⊥AB,且AB=2AD=2,M,N分别为AB,CD中点.
如图,多面体ABCDS中,四边形ABCD为矩形,SD⊥AD,SD⊥AB,且AB=2AD=2,M,N分别为AB,CD中点.