题目内容
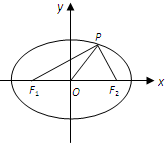如图，F1，F2分别为椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：与椭圆两个焦点有关的问题，一般以回归定义求解为上策，抓住△PF1F2为直角三角形建立等式关系．
解答：
解：由题意：
c2=
，则c=2，∴P（1，
）
代入椭圆方程
+
=1，得
+
=1，求出b2=2
．
| ||
| 4 |
| 3 |
| 3 |
代入椭圆方程
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| b2+4 |
| 3 |
| b2 |
| 3 |
点评：本题考查了椭圆的基本量，关键抓住图形特征建立等式关系，考查计算能力．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
设圆C的方程为x2+y2-2x-2y-2=0，直线l的方程为（m+1）x-my-1=0，圆C被直线l截得的弦长等于（ ）
| A、4 | ||
B、2
| ||
| C、2 | ||
| D、与m有关 |
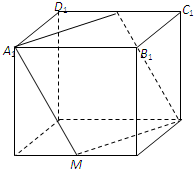在棱长为a的正方体ABCD-A1B1C1D1中，M是棱AB的中点，过A1，M，C三点的平面交棱C1D1于N点，
在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是直角梯形，AB∥CD，∠BAD=90°，AB=AD=PD=1，CD=2．