题目内容
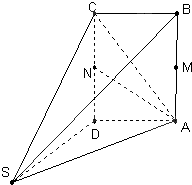如图，多面体ABCDS中，四边形ABCD为矩形，SD⊥AD，SD⊥AB，且AB=2AD=2，M，N分别为AB，CD中点．（1）求异面直线SM，AN所成的角；
（2）若二面角A-SC-D大小为60°，求SD的长．
考点：与二面角有关的立体几何综合题,异面直线及其所成的角
专题：空间角
分析：（1）几何法：由三垂线定理得，SM⊥AN，∴直线SM，AN所成的角90°；
向量法：以D为原点，分别以DS，DA，DC为x，y，z轴建系，
•
=0，故SM与AN成90°角；
（2）几何法：过D作DE⊥SC于E，连AE则∠AED为所求二面角A-SC-D的平面角60°，后解三角形；向量法：设平面ASC的一个法向量为
，平面SDC的一个法向量为
，二面角A-SC-D大小为60°，求得坐标中的参数即可．
向量法：以D为原点，分别以DS，DA，DC为x，y，z轴建系，
| AN |
| SM |
（2）几何法：过D作DE⊥SC于E，连AE则∠AED为所求二面角A-SC-D的平面角60°，后解三角形；向量法：设平面ASC的一个法向量为
| n1 |
| n2 |
解答：
法一（几何法）：（1）解：∵SD⊥AD，SD⊥AB，
∴SD⊥面ABCD，连接MN，则由已知，AMND为正方形，
连DM，则DM⊥AN，
又DM是SM在面ABCD上的射影，由三垂线定理得，SM⊥AN，
∴直线SM，AN所成的角90°；
（2）∵AD⊥CD，AD⊥SD，
∴AD⊥面SCD，过D作DE⊥SC于E，连AE则∠AED为所求二面角A-SC-D的平面角60°则在R△ADE中易得DE=
，
设SD=a，在Rt△SDC中，DE=
=
，∴SD=a
．
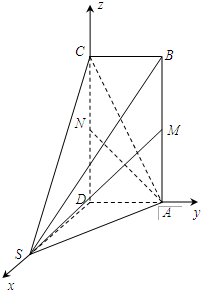
法二：（向量法）解：（1）以D为原点，分别以DS，DA，DC为x，y，z轴建系，
则A（0，1，0），N（0，0，1），M（0，1，1），C（0，0，2），
设S（a，0，0），则
=（0，-1，1），
=（-a，1，1），
•
=0，
故SM与AN成90°角；
（2）设平面ASC的一个法向量为
=（x，y，z）
=（a，-1，0），
=（0，-1，2），
由
，⇒
=（2，2a，a），
又平面SDC的一个法向量为
=（0，1，0），
由题意：cos60°=|cos＜
，
＞|=
，
∴SD=a=
．
法一（几何法）：（1）解：∵SD⊥AD，SD⊥AB，∴SD⊥面ABCD，连接MN，则由已知，AMND为正方形，
连DM，则DM⊥AN，
又DM是SM在面ABCD上的射影，由三垂线定理得，SM⊥AN，
∴直线SM，AN所成的角90°；
（2）∵AD⊥CD，AD⊥SD，
∴AD⊥面SCD，过D作DE⊥SC于E，连AE则∠AED为所求二面角A-SC-D的平面角60°则在R△ADE中易得DE=
| ||
| 3 |
设SD=a，在Rt△SDC中，DE=
| 2a | ||
|
| ||
| 3 |
2
| ||
| 11 |
法二：（向量法）解：（1）以D为原点，分别以DS，DA，DC为x，y，z轴建系，
则A（0，1，0），N（0，0，1），M（0，1，1），C（0，0，2），
设S（a，0，0），则
| AN |
| SM |
| AN |
| SM |
故SM与AN成90°角；
（2）设平面ASC的一个法向量为
| n1 |
| AS |
| AC |
由
|
| n1 |
又平面SDC的一个法向量为
| n2 |
由题意：cos60°=|cos＜
| n1 |
| n2 |
| 2a | ||
|
∴SD=a=
2
| ||
| 11 |
点评：本题考查异面直线所成的角，二面角的平面角，即可用几何法，也可向量法，两种方法都要熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是直角梯形，AB∥CD，∠BAD=90°，AB=AD=PD=1，CD=2．