题目内容
设函数f(x)=x2-2(-1)klnx(k∈N*),f′(x)表示f(x)的导函数.
(1)求函数y=f(x)的单调递增区间;
(2)当k为偶数时,若函数f(x)的图象恒在函数g(x)=(1-2a)x2的上方,求实数a的取值范围;
(3)当k为奇数时,设bn=
f′(n)-n,数列{bn}的前n项和为Sn,证明不等式(1+bn)
>e对一切正整数n均成立,并比较S2014-2与ln2014的大小.
(1)求函数y=f(x)的单调递增区间;
(2)当k为偶数时,若函数f(x)的图象恒在函数g(x)=(1-2a)x2的上方,求实数a的取值范围;
(3)当k为奇数时,设bn=
| 1 |
| 2 |
| 1 |
| bn+1 |
考点:数列与不等式的综合,利用导数研究函数的极值,数列的求和
专题:综合题,等差数列与等比数列,不等式的解法及应用
分析:(1)先求函数f(x)的导数,f′(x),再对k进行奇偶数讨论:①当k 为奇数时;②当k 为偶数时,分别得出导数值为正或负时的x的取值集合,最后综合即可;
(2)由题意知:x2-2lnx>(1-2a)x2恒成立,即a>
恒成立,设h(x)=
,则a>[h(x)]max;
(3)当k为奇数时,f′(x)=2(x+
),要证(1+bn)
>e,即证(1+
)n+1>e,两边取对数,即证ln(1+
)>
,设1+
=t,则n=
(t>1),即证不等式lnt>1-
(t>1)成立.构造函数.利用导数工具研究其单调性即可证得lnt>1-
,最后利用累乘法即可证出S2014-1<ln2014.
(2)由题意知:x2-2lnx>(1-2a)x2恒成立,即a>
| lnx |
| x2 |
| lnx |
| x2 |
(3)当k为奇数时,f′(x)=2(x+
| 1 |
| x |
| 1 |
| bn+1 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| t-1 |
| 1 |
| t |
| 1 |
| t |
解答:
(1)解:函数的定义域为(0,+∞),
又y′=f′(x)=2x-2(-1)k
=
,…(1分)
①当k为奇数时,f′(x)=
,∵x∈(0,+∞),∴f'(x)>0在(0,+∞)恒成立.
即f'(x)的单调递增区间为(0,+∞)…(2分)
②当k为偶数时,f′(x)=
=
又x∈(0,+∞),∴x+1>0
由f'(x)>0,得x-1>0,∴x>1,即f(x)的单调递增区间为(1,+∞),
综上所述:当k为奇数时,f(x)的单调递增区间为(0,+∞),
当k为偶数时,f(x)的单调递增区间为(1,+∞)…(4分)
(2)解:当k为偶数时,f(x)=x2-2lnx,
由题意知:x2-2lnx>(1-2a)x2恒成立,即a>
恒成立.
设h(x)=
,则a>[h(x)]max…(6分)
由h′(x)=
=0得x=
,h'(x),h(x)随x的变化情况如下表:
∴h(x)在x=
处取得极大值,也为最大值,
即[h(x)]max=h(
)=
,故实数a的取值范围为a>
…(9分)
(3)证明:由(1)知,当k为奇数时,f′(x)=2(x+
),
∴bn=
f′(n)-n=
,Sn=1+
+
+…+
.
由已知要证(1+
)n+1>e,两边取自然对数,即证ln(1+
)>
,…(11分)
设1+
=t,则n=
(t>1),即证不等式lnt>1-
(t>1)成立.
构造函数ϕ(t)=lnt+
-1(t>1),下面证明ϕ(t)在(1,+∞)上恒大于0.
∵t>1,∴ϕ′(t)=
-
>0
∴ϕ(t)在(1,+∞)上单调递增,∴ϕ(t)>ϕ(1)=0
即lnt>1-
,∴ln(1+
)>
,∴(1+
)n+1>e,
即(1+bn)
>e成立…(13分)
由ln
>
,得
+
+…+
<ln
+ln
+…+ln
=ln(n+1),
即Sn+1-1<ln(n+1),当n=2013时,S2014-1<ln2014…(14分)
又y′=f′(x)=2x-2(-1)k
| 1 |
| x |
| 2[x2-(-1)k] |
| x |
①当k为奇数时,f′(x)=
| 2(x2+1) |
| x |
即f'(x)的单调递增区间为(0,+∞)…(2分)
②当k为偶数时,f′(x)=
| 2(x2-1) |
| x |
| 2(x+1)(x-1) |
| x |
由f'(x)>0,得x-1>0,∴x>1,即f(x)的单调递增区间为(1,+∞),
综上所述:当k为奇数时,f(x)的单调递增区间为(0,+∞),
当k为偶数时,f(x)的单调递增区间为(1,+∞)…(4分)
(2)解:当k为偶数时,f(x)=x2-2lnx,
由题意知:x2-2lnx>(1-2a)x2恒成立,即a>
| lnx |
| x2 |
设h(x)=
| lnx |
| x2 |
由h′(x)=
| 1-2lnx |
| x3 |
| e |
| x | (0,
|
| (
| ||||||
| h'(x) | + | 0 | - | ||||||
| h(x) | 极大值 |
| e |
即[h(x)]max=h(
| e |
| 1 |
| 2e |
| 1 |
| 2e |
(3)证明:由(1)知,当k为奇数时,f′(x)=2(x+
| 1 |
| x |
∴bn=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
由已知要证(1+
| 1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
设1+
| 1 |
| n |
| 1 |
| t-1 |
| 1 |
| t |
构造函数ϕ(t)=lnt+
| 1 |
| t |
∵t>1,∴ϕ′(t)=
| 1 |
| t |
| 1 |
| t2 |
∴ϕ(t)在(1,+∞)上单调递增,∴ϕ(t)>ϕ(1)=0
即lnt>1-
| 1 |
| t |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
即(1+bn)
| 1 |
| bn+1 |
由ln
| n+1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
即Sn+1-1<ln(n+1),当n=2013时,S2014-1<ln2014…(14分)
点评:本小题主要考查利用导数研究函数的单调性、证明不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于难题.

练习册系列答案
相关题目
有A、B两个口袋,A袋装有4个白球,2个黑球;B袋装有3个白球,4个黑球,从A袋、B袋各取2个球交换之后,则A袋中装有4个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=log(x-1)(3-x)的定义域是( )
| A、(1,2)∪(3,4) |
| B、[1,2]∪[3,4] |
| C、(1,2)∪(2,3) |
| D、[1,2]∪[2,3] |
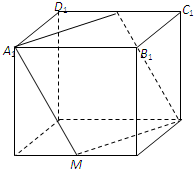 在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,
在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,