题目内容
曲线f(x)=x2+alnx在点(1,f(1))处的切线斜率为4,则a= .
考点:利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:由求导公式求导函数,由题意得求出f′(1)=4,代入求出a的值.
解答:
解:由题意得f(x)=x2+alnx,则f′(x)=2x+
,
因为在点(1,f(1))处的切线斜率为4,
所以f′(1)=4,即2+a=4,解得a=2,
故答案为:2.
| a |
| x |
因为在点(1,f(1))处的切线斜率为4,
所以f′(1)=4,即2+a=4,解得a=2,
故答案为:2.
点评:本题考查导数的几何意义,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 某同学进入高二前,高一年的四次期中、期末测试的数学成绩的茎叶图如图所示,则该同学数学成绩的平均数是( )
某同学进入高二前,高一年的四次期中、期末测试的数学成绩的茎叶图如图所示,则该同学数学成绩的平均数是( )| A、125 | B、126 |
| C、127 | D、128 |
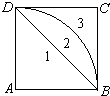 正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧
正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧 |
| DB |
| A、2:1:1 |
| B、1:2:1 |
| C、1:1:1 |
| D、2:2:1 |
若函数f(x)=
x2-x+
,x∈[1,b]的值域也为[1,b],则b的值为( )
| 1 |
| 2 |
| 3 |
| 2 |
| A、1或3 | ||
B、1或
| ||
C、
| ||
| D、3 |
函数f(x)=x3-x-3的零点所在区间是( )
| A、[-1,0] |
| B、[0,1] |
| C、[1,2] |
| D、[2,3] |
函数y=x4-4x+3在区间[-1,2]上的最大值为( )
| A、11 | B、8 | C、12 | D、0 |
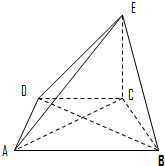 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.