题目内容
过点P（-2，-3）作圆C：（x-4）2+﹙y-2﹚2=9的两条切线，切点分别是A、B．求线段AB的长．
考点：圆的切线方程
专题：直线与圆
分析：由题意求得PC和cos∠PCA=
的值，可得cos2∠PCA=2cos2∠PCA-1的值，△ABC中，再利用余弦定理求得AB的值．
| R |
| PC |
解答：
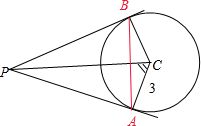解：由题意可得，圆心C（4，2），半径为R=3，
求得PC=
=
，∴cos∠PCA=
=
，
∴cos2∠PCA=2cos2∠PCA-1=-
．
∴AB2=R2+R2-2R•R•cos2∠PCA=9+9-18×（-
）=
，
∴AB=
=
．
解：由题意可得，圆心C（4，2），半径为R=3，求得PC=
| (4+2)2+(2+3)2 |
| 61 |
| R |
| PC |
| 3 | ||
|
∴cos2∠PCA=2cos2∠PCA-1=-
| 43 |
| 61 |
∴AB2=R2+R2-2R•R•cos2∠PCA=9+9-18×（-
| 43 |
| 61 |
| 18×104 |
| 61 |
∴AB=
|
12
| ||
| 61 |
点评：本题主要考查直线和圆相切的性质，二倍角的余弦公式、余弦定理的应用，属于中档题．
练习册系列答案
名题金卷系列答案
相关题目
在花园小区内有一块三边长分别为3米、4米、5米的三角形绿化地，有一只小狗在其内部玩耍，若不考虑小狗的大小，则在任意指定的某时刻，小狗与三角形三个顶点的距离均超过1米的概率是（ ）
A、1-
| ||
B、1-
| ||
C、2-
| ||
D、2-
|
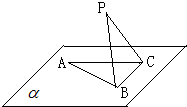如图，△ABC在平面α内，∠ACB=90°，AB=2BC=2，P为平面α外一个动点，且PC=
在△ABC中，AD为BC边上的高，已知：AC=b；AB=c，AD=BC，求