题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c.角A为锐角,且满足3b=5asinB.
(1)求sin2A+cos2
的值;
(2)若a=
,△ABC的面积为
,求b,c.
(1)求sin2A+cos2
| B+C |
| 2 |
(2)若a=
| 2 |
| 3 |
| 2 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(1)根据正弦定理将条件进行化简,得到sinA=
,然后利用倍角公式即可得到三角函数的值.
(2)根据三角形的面积公式,以及余弦定理,建立方程组解方程组即可得到结论.
| 3 |
| 5 |
(2)根据三角形的面积公式,以及余弦定理,建立方程组解方程组即可得到结论.
解答:
解:(1)∵3b=5asinB.
∴由正弦定理可得3sinB=5sinAsinB.
∵sinB≠0,
∴sinA=
,
∵角A为锐角,
∴cosA=
.
则sin2A+cos2
=2sinAcosA+
═2sinAcosA+
-cosA=2×
×
+
-
×
=
.
(2)若a=
,△ABC的面积为
,
则
bcsinA=
bc×
=
,
即bc=5
由余弦定理得a2=b2+c2-2bccosA,
即2=b2+c2-2×5×
,
∴b2+c2=10,解得b=c=
.
∴由正弦定理可得3sinB=5sinAsinB.
∵sinB≠0,
∴sinA=
| 3 |
| 5 |
∵角A为锐角,
∴cosA=
| 4 |
| 5 |
则sin2A+cos2
| B+C |
| 2 |
| 1+cos(B+C) |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 53 |
| 50 |
(2)若a=
| 2 |
| 3 |
| 2 |
则
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
即bc=5
由余弦定理得a2=b2+c2-2bccosA,
即2=b2+c2-2×5×
| 4 |
| 5 |
∴b2+c2=10,解得b=c=
| 5 |
点评:本题主要考查三角函数的化简与求值,利用正弦定理,余弦定理以及三角形的面积公式,建立方程组是解决本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
已知一只蚂蚁在圆:x2+y2=1的内部任意随机爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁爬行在区域|x|+|y|≤1内的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
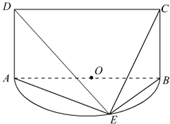 如图,E是以AB为直径的半圆O上异于A、B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2a.
如图,E是以AB为直径的半圆O上异于A、B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2a.