Question

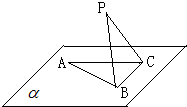如图，△ABC在平面α内，∠ACB=90°，AB=2BC=2，P为平面α外一个动点，且PC=

3

，∠PBC=60°
（Ⅰ）问当PA的长为多少时，AC⊥PB．
（Ⅱ）当△PAB的面积取得最大值时，求直线PC与平面PAB所成角的正弦值．

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：（Ⅰ）由已知条件推导出AC⊥BC，当AC⊥PC时，AC⊥平面PBC，由此能求出当PA=

6

时，AC⊥PB．
（Ⅱ）由已知条件推导出当△PAB的面积取得最大值时，∠PBA=90°．过C作CE⊥BD，E为垂足，由题意得到∠CPE就是直线PC与平面PAB所成角，由此能求出直线PC与平面PAB所成角的正弦值．

解答： （本小题满分15分）
解：（Ⅰ）∵∠ACB=90°，∴AC⊥BC，
当AC⊥PC时，AC⊥平面PBC，而PB?平面PBC
AC⊥PB时，PA=

AC2+PC2

=

3+3

=

6

，
即当PA=

6

时，AC⊥PB．
（Ⅱ）在△PBC中，∵PC=

3

，∠PBC=60°，BC=1，
∴BC⊥PC，PB=2．当△PAB的面积取得最大值时，∠PBA=90°，
如图，在Rt△PBA中，∵BP=BA=2，∴BD=

2

，
又在Rt△BCD中，∵BC=1，∴CD=1，
过C作CE⊥BD，E为垂足，由于PA⊥平面BCD，
∴平面BCD⊥平面PBA，由两个平面互相垂直的性质可知：CE⊥平面PBA，
∴∠CPE就是直线PC与平面PAB所成角，
在Rt△BCD中，CE=

BC•CD

BD

=

1×1

2

=

2

2

，
在Rt△PEC中，sin∠CPE=

CE

PC

=

2

2

÷

3

=

6

6

，
∴直线PC与平面PAB所成角的正弦值是

6

6

．

点评：本题考查异面直线垂直的条件的应用，考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意空间思维能力的培养．