题目内容
已知函数f(x)=x2+ax+2且sinα,sin(α+
)是函数y=f(x)-
x-
的两个零点,其中α∈(0,
).
(1)求a的值;
(2)若g(x)=2ex(x+1)对任意x≥-2,f(x)≤kg(x)恒成立,求k的取值范围.
| π |
| 3 |
| 11 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
(1)求a的值;
(2)若g(x)=2ex(x+1)对任意x≥-2,f(x)≤kg(x)恒成立,求k的取值范围.
考点:函数恒成立问题,两角和与差的正弦函数
专题:导数的综合应用
分析:(1)根据韦达定理得到sinα+sin(α+
)=
-a,sinα•sin(α+
)=
,再根据三角函数中的积化和差求出α的值,继而求出a的值,
(2)构造函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2,再求导,需要分类讨论,利用导数求出函数的最小值,问题得以解决.
| π |
| 3 |
| 11 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
(2)构造函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2,再求导,需要分类讨论,利用导数求出函数的最小值,问题得以解决.
解答:
解:(1)∵f(x)=x2+ax+2,函数y=f(x)-
x-
,
∴y=x2+ax+2-
x-
=x2-(
-a)x+
,
∴sinα+sin(α+
)=
-a,sinα•sin(α+
)=
,
∵sinα•sin(α+
)=
[cos
-cos(2α+
)]=
,
∴cos(2α+
)=-
,
∵α∈(0,
).
∴2α+
∈(
,
),
∴2α+
=
,
∴α=
,
∴sinα+sin(α+
)=sin
+sin(
+
)=
=
-a,
∴a=4,
(2)由(1)知,f(x)=x2+4x+2,g(x)=2ex(x+1).
设函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2,
则F′(x)=2kex(x+2)-2x-4=2(x+2)(kex-1).
(ⅰ)若1≤k<e2,则-2<x1≤0,从而当x∈(-2,x1)时,F′(x)<0;
当x∈(x1,+∞)时,F′(x)>0,即F(x)在(-2,x1)上单调递减,在(x1,+∞)上单调递增,
故F(x)在[-2,+∞)上的最小值为F(x1).
而F(x1)=2x1+2-x-4x1-2=-x1(x1+2)≥0.
故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.
(ⅱ)若k=e2,则F′(x)=2e2(x+2)(ex-e-2).
从而当x>-2时,F′(x)>0,即F(x)在(-2,+∞)上单调递增.而F(-2)=0,
故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.
综上所述,k的取值范围为[1,e2]
| 11 |
| 2 |
| 3 |
| 2 |
∴y=x2+ax+2-
| 11 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
∴sinα+sin(α+
| π |
| 3 |
| 11 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
∵sinα•sin(α+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴cos(2α+
| π |
| 3 |
| 1 |
| 2 |
∵α∈(0,
| π |
| 2 |
∴2α+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴2α+
| π |
| 3 |
| 2π |
| 3 |
∴α=
| π |
| 6 |
∴sinα+sin(α+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 3 |
| 2 |
| 11 |
| 2 |
∴a=4,
(2)由(1)知,f(x)=x2+4x+2,g(x)=2ex(x+1).
设函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2,
则F′(x)=2kex(x+2)-2x-4=2(x+2)(kex-1).
(ⅰ)若1≤k<e2,则-2<x1≤0,从而当x∈(-2,x1)时,F′(x)<0;
当x∈(x1,+∞)时,F′(x)>0,即F(x)在(-2,x1)上单调递减,在(x1,+∞)上单调递增,
故F(x)在[-2,+∞)上的最小值为F(x1).
而F(x1)=2x1+2-x-4x1-2=-x1(x1+2)≥0.
故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.
(ⅱ)若k=e2,则F′(x)=2e2(x+2)(ex-e-2).
从而当x>-2时,F′(x)>0,即F(x)在(-2,+∞)上单调递增.而F(-2)=0,
故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.
综上所述,k的取值范围为[1,e2]
点评:本题考查导数在最大值与最小值问题中的应用以及三角函数的关系,解题的关键是利用导数研究出函数的单调性,判断出函数的最值,恒成立的问题一般转化最值问题来求解,本题即转化为用单调性求函数在闭区间上的最值的问题,求出最值再判断出参数的取值.本题运算量过大,解题时要认真严谨,避免变形运算失误,导致解题失败.

练习册系列答案
相关题目
设集合A={0,1},B={-1,0,m-2},若A⊆B,则实数m=( )
| A、0 | B、1 | C、2 | D、3 |
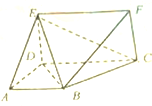 如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.
如图所示,直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=1,CD=2.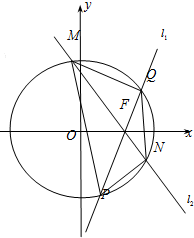 已知椭圆
已知椭圆