Question

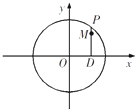如图，设P是圆x²+y²=25上的动点，点D是P在x轴上的投影，M为PD上一点，且|MD|=

4

5

|PD|．
（1）当P在圆上运动时，求点M的轨迹C的方程；
（2）若直线y=ax-5与曲线C交于A，B两点，且OA⊥OB，求a的值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设M的坐标为（x，y），P的坐标为（x_P，y_P），由已知得

xP=x yP= 5 4 y.

由此能求出C的方程．
（2）设A（x₁，y₁），B（x₂，y₂），由

16x2+25y2=400 y=ax-5

，得（16+25a²）x²-250ax+225=0，由此利用韦达定理和根的判别式能求出a的值．

解答： 解：（1）设M的坐标为（x，y），P的坐标为（x_P，y_P），
∵P是圆x²+y²=25上的动点，点D是P在x轴上的投影，M为PD上一点，且|MD|=

4

5

|PD|，
∴

xP=x yP= 5 4 y.

∵P在圆上，∴x2+(

5

4

y)2=25，即C的方程为

x2

25

+

y2

16

=1．…（4分）
（2）设A（x₁，y₁），B（x₂，y₂），
由

16x2+25y2=400 y=ax-5

，得（16+25a²）x²-250ax+225=0，
∴x1+x2=

250a

16+25a2

，x1x2=

225

16+25a2

①…（8分）
由

OA

•

OB

=0，得x₁x₂+y₁y₂=0，
即（1+a²）x₁x₂-5a（x₁+x₂）+25=0②
将①代入②式得

225(1+a2)-1250a2+25(16+25a2)

16+25a2

=0
解得a=

5

4

，经验满足△＞0，
∴a=

5

4

．…（12分）

点评：本题考查点的轨迹方程的求法，考查实数值的求法，解题时要认真审题，注意韦达定理和根的判别式的合理运用．