题目内容
已知某二次函数图象的顶点为A(2,-18),它与x轴两个交点之间的距离为6,则该二次函数的解析式为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:因为二次函数f(x)图象顶点是(2,-18),故可设f(x)=a(x-2)2-18,函数图象的对称轴是x=2,图象与x轴的两个交点的距离是6,由此可求出函数图象与x轴交点的坐标,进而由此能求出f(x)的解析式.
解答:
解:∵二次函数f(x)图象顶点是(2,-18),
故可设f(x)=a(x-2)2-18,
∵函数图象的对称轴是x=2,图象与x轴的两个交点的距离是6,
故点(5,0),(-1,0)在f(x)图象上.
∴f(5)=a(5-2)2-18=0,
解得a=2,
∴f(x)=2x2-8x-10.
故答案为:f(x)=2x2-8x-10
故可设f(x)=a(x-2)2-18,
∵函数图象的对称轴是x=2,图象与x轴的两个交点的距离是6,
故点(5,0),(-1,0)在f(x)图象上.
∴f(5)=a(5-2)2-18=0,
解得a=2,
∴f(x)=2x2-8x-10.
故答案为:f(x)=2x2-8x-10
点评:本题考查二次函数的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知i是虚数单位,复数z=
,则z的共轭复数
等于( )
| 4+3i |
| 1+2i |
. |
| z |
| A、-2+i | B、-2-i |
| C、2+i | D、2-i |
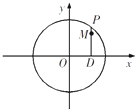 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且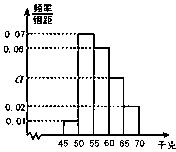 为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.则a=
为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.则a=