题目内容

已知等比数列{an}中，a3+a5=8，a1a5=4，则
a13
a9
=
 
．
考点：等比数列的性质
专题：等差数列与等比数列
分析：由等比数列的性质可得a1a5=a32=4，解出a3，分别可得q2，而
a13
a9
=q4，代入可得答案．
解答： 解：由等比数列的性质可得a1a5=a32=4，
解得a3=2，或a3=-2，
当a3=2时，可得a5=8-a3=6，q2=
a5
a3
=3
当a3=-2，可得a5=8-a3=10，q2=
a5
a3
=-5，（舍去）
∴
a13
a9
=q4=32=9
故答案为：9
点评：本题考查等比数列的性质，涉及分类讨论的思想，属基础题．
练习册系列答案
相关题目
已知抛物线C1：y2=2px（p＞0）的焦点F以及椭圆C2：
y2
a2
+
x2
b2
=1（a＞b＞0）的上、下焦点及左、右顶点均在圆O：x2+y2=1上．
（1）求抛物线C1和椭圆C2的标准方程；
（2）过点F的直线交抛物线C1于A，B两不同点，交y轴于点N，已知
NA
=λ1
AF
，
NB
=λ2
BF
，则λ1+λ2是否为定值？若是，求出其值；若不是，说明理由．
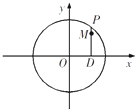如图，设P是圆x2+y2=25上的动点，点D是P在x轴上的投影，M为PD上一点，且|MD|=
4
5
|PD|．
（1）当P在圆上运动时，求点M的轨迹C的方程；
（2）若直线y=ax-5与曲线C交于A，B两点，且OA⊥OB，求a的值．
设函数y=f（x）的定义域为R，若对于给定的正数k，定义函数fk（x）=
k，f(x)≤k
f(x)，f(x)＞k
则当函数f（x）=
1
x
，k=1时，定积分
∫
2
1
4
fk（x）dx的值为
 
．
已知f（x）=x2-2x-3，则下列关于x的方程f（|x|）=k的根的个数说法中正确的有
 

①存在实数k，使得方程f（|x|）=k有2个根；
②存在实数k，使得方程f（|x|）=k有4个根；
③存在实数k，使得方程f（|x|）=k有5个根；
④存在实数k，使得方程f（|x|）=k有6个根．
某同学在7天内每天参加体育锻炼的时间（单位：分钟）用茎叶图表示如图，图中左列表示时间的十位数，右列表示时间的个位数．则这7天该同学每天参加体育锻炼时间（单位：分钟）的平均数为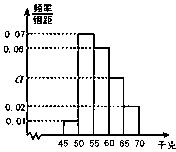
 
．
为了解学生的身体状况，某校随机抽取了一批学生测量体重．经统计，这批学生的体重数据（单位：千克）全部介于45至70之间．将数据分成以下5组：第1组[45，50），第2组[50，55），第3组[55，60），第4组[60，65），第5组[65，70]，得到如图所示的频率分布直方图．则a=
 
，现采用分层抽样的方法，从第3，4，5组中随机抽取6名学生，则第3，4，5组抽取的学生人数依次为
 
．
己知集合A={x|x2-3x+2＜0}，B={x|log4x＞
1
2
}，则（　　）
A、A∩B=∅
B、B⊆A
C、A∩∁RB=R
D、A⊆B
已知二次函数f（x）=ax2+bx+c（a＞0），满足a+b+c＜0，则方程f（x）=0的两根x1，x2一定满足（　　）
A、x1＜1且x2＜1
B、x1＞1且x2＞1
C、x1，x2中一个大于1，另一个小于1
D、x1+x2＜1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网