题目内容
已知变量x,y满足约束条件
,若z=kx+y的最大值为5,则实数k= .
|
考点:简单线性规划的应用
专题:不等式的解法及应用
分析:画出满足约束条件
的平面区域,然后分析平面区域里各个角点,进一步利用目标函数z=kx+y的最大值为11,判断目标函数经过的点,即可求出k的值.
|
解答:
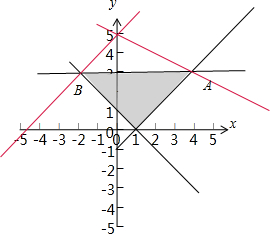 解:由变量x,y满足约束条件
解:由变量x,y满足约束条件
,作出可行域:
∵z=kx+y的最大值为5,即y=-kx+z在y轴上的截距是5,
∴目标函数z=kx+y经过
的交点B(-2,3),
∴5=k×(-2)+3;解得k=-1.
目标函数z=kx+y经过
的交点A(4,3),
∴5=4k+3;解得k=
.
故答案为:-1或
.
 解:由变量x,y满足约束条件
解:由变量x,y满足约束条件
|
∵z=kx+y的最大值为5,即y=-kx+z在y轴上的截距是5,
∴目标函数z=kx+y经过
|
∴5=k×(-2)+3;解得k=-1.
目标函数z=kx+y经过
|
∴5=4k+3;解得k=
| 1 |
| 2 |
故答案为:-1或
| 1 |
| 2 |
点评:本题考查简单的线性规划的应用,在解决线性规划的小题时,常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在半径为2的圆内随机地取一点A,以点A为中点做一条弦PQ,求弦PQ长超过圆内接正三角形的边长概率是多少( )
A、
| ||
B、
| ||
C、
| ||
D、
|
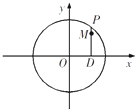 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且 某同学在7天内每天参加体育锻炼的时间(单位:分钟)用茎叶图表示如图,图中左列表示时间的十位数,右列表示时间的个位数.则这7天该同学每天参加体育锻炼时间(单位:分钟)的平均数为
某同学在7天内每天参加体育锻炼的时间(单位:分钟)用茎叶图表示如图,图中左列表示时间的十位数,右列表示时间的个位数.则这7天该同学每天参加体育锻炼时间(单位:分钟)的平均数为