题目内容
设f（x）=asinωx+bcosωx（ω＞0）的周期T=π，最大值f（
）=4．
（1）求ω，a，b的值；
（2）若α，β为方程f（x）=0的两根，α，β终边不共线，求tan（α+β）的值．
| π |
| 12 |
（1）求ω，a，b的值；
（2）若α，β为方程f（x）=0的两根，α，β终边不共线，求tan（α+β）的值．
考点：两角和与差的正弦函数,两角和与差的正切函数
专题：三角函数的求值
分析：（1）由f(x)=
sin(ωx+ϕ)，T=π=
，求得ω=2．再根据f（x）的最大值为f（
）=4，可得4=
①，且asin
+bcos
=4 ②，由①、②解出a、b的值．
（2）由题意可得f（α）=f（β）=0，故有4sin(2α+
)=4sin(2β+
)，由此求得α+β=kπ+
，k∈z，可得tan（α+β）的值．
| a2+b2 |
| 2π |
| ω |
| π |
| 12 |
| a2+b2 |
| π |
| 6 |
| π |
| 6 |
（2）由题意可得f（α）=f（β）=0，故有4sin(2α+
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
解答：
解：（1）由于f(x)=
sin(ωx+ϕ)，∴T=π=
，∴ω=2．
又∵f（x）的最大值为f（
）=4，∴4=
①，且asin
+bcos
=4 ②，
由 ①、②解出 a=2，b=2
，f（x）=2sin2x+2
cos2x．
（2）∵f(x)=2sin2x+2
cos2x=4sin(2x+
)，∴由题意可得f（α）=f（β）=0，∴4sin(2α+
)=4sin(2β+
)，
∴2α+
=2kπ+2β+
，或 2α+
=2kπ+π-(2β+
)，
即α=kπ+β（α，β共线，故舍去）或α+β=kπ+
，∴tan(α+β)=tan(kπ+
)=
（k∈Z）．
| a2+b2 |
| 2π |
| ω |
又∵f（x）的最大值为f（
| π |
| 12 |
| a2+b2 |
| π |
| 6 |
| π |
| 6 |
由 ①、②解出 a=2，b=2
| 3 |
| 3 |
（2）∵f(x)=2sin2x+2
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴2α+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
即α=kπ+β（α，β共线，故舍去）或α+β=kπ+
| π |
| 6 |
| π |
| 6 |
| ||
| 3 |
点评：本题主要考查三角恒等变换，三角函数的周期性，解三角方程，属于基础题．
练习册系列答案
相关题目
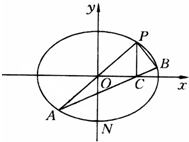如图，在平面直角坐标系xOy中，过坐标原点的直线交椭圆