题目内容
已知a1=1，an+1=
，求an．
| 2an |
| 3an+1 |
考点：数列递推式
专题：等差数列与等比数列
分析：把数列递推式取倒数，得到
=
•
+
，然后构造出等比数列{
-3}，求其通项公式后可得an．
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
| 3 |
| 2 |
| 1 |
| an |
解答：
解：由an+1=
，得
=
•
+
，
即
-3=
(
-3)．
∵a1=1，
∴
-3=-2．
则数列{
-3}构成以-2为首项，以
为公比的等比数列．
∴
-3=-2•(
)n-1，
∴an=
．
| 2an |
| 3an+1 |
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
| 3 |
| 2 |
即
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
∵a1=1，
∴
| 1 |
| a1 |
则数列{
| 1 |
| an |
| 1 |
| 2 |
∴
| 1 |
| an |
| 1 |
| 2 |
∴an=
| 2n-2 |
| 3•2n-2-1 |
点评：本题考查了数列递推式，考查了等比关系的确定，考查了等比数列通项公式的求法，是中档题．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
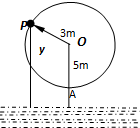如图为一半径为3米的水轮，水轮圆心O距水面5米，已知水轮每分钟逆时针转6圈，水轮上的固定点P到水面距离y（米）与时间x（秒）满足关系式y=Asin（ωx+φ）+b的函数形式，当水轮开始转动时P点位于距离水面最近的A点处，则A=