题目内容
设f(x)=
,则满足f(x)=
的x的值为 .
|
|
| 1 |
| 4 |
考点:函数的零点
专题:函数的性质及应用
分析:根据分段函数,解方程即可解出x的值.
解答:
解:由分段函数可知,
若x>1,则由f(x)=
得:
log81x=
,即x=81
=34×
=3.
若x≤1,则由f(x)=
得:
2-x=
,
即(
)x=(
)2,解得x=2,不满足条件,
故x=3.
故答案为:3.
若x>1,则由f(x)=
| 1 |
| 4 |
log81x=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
若x≤1,则由f(x)=
| 1 |
| 4 |
2-x=
| 1 |
| 4 |
即(
| 1 |
| 2 |
| 1 |
| 2 |
故x=3.
故答案为:3.
点评:本题主要考查分段函数的应用,利用分段函数解方程即可,注意讨论变量x的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
+log2(x+2)的定义域为( )
| 3-x |
| A、(-∞,3] |
| B、(-2,3) |
| C、(-2,3] |
| D、(-∞,-2)∪[3,+∞) |
已知区域M:x2+y2≤4,区域N:-x≤y≤x,随机向区域M中投放一点.该点落在区域N内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
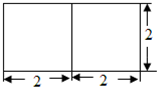 已知一个三棱柱的底面是正三角形、侧棱垂直于底面,其正视图如图所示,则这个三棱柱的体积为
已知一个三棱柱的底面是正三角形、侧棱垂直于底面,其正视图如图所示,则这个三棱柱的体积为