题目内容
经市场调查,东方百货超市的一种商品在过去的一个月内(以30天计算),销售价格f(t)与时间(天)的函数关系近似满足f(t)=100(1+
),销售量g(t)与时间(天)的函数关系近似满足g(t)=
.
(1)试写出该商品的日销售金额W(t)关于时间t(1≤t≤30,t∈N)的函数表达式;
(2)求该商品的日销售金额W(t)的最大值与最小值.
| 1 |
| t |
|
(1)试写出该商品的日销售金额W(t)关于时间t(1≤t≤30,t∈N)的函数表达式;
(2)求该商品的日销售金额W(t)的最大值与最小值.
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:(1)利用W(t)=g(t)f(t),结合已知解析式,可得分段函数;
(2)利用(1)中函数,分类讨论,根据函数的单调性,可得日销售金额W(t)的最大值与最小值.
(2)利用(1)中函数,分类讨论,根据函数的单调性,可得日销售金额W(t)的最大值与最小值.
解答:
解:(1)当1≤t<25时,W(t)=g(t)f(t)=100(100+t)(1+
)=100(t+
+101);
当25≤t≤30时,W(t)=g(t)f(t)=100(150-t)(1+
)=100(
-t+149);
所以W(t)=
(t∈N)…(6分)
(2)(i)当1≤t<25时,由双勾函数的性质知W(t)=100(t+
+101)在区间[1,10]上单减,在区间[10,25)上单增,
因为W(10)=12100,W(1)=20200,W(25)=13000,
所以当t=10时,W(t)最小值为12100,当t=1时,W(t)最大值为20200;…(9分)
(ii)当25≤t≤30时,W(t)=100(
-t+149),y=
和y=-t在[25,30]单减,则
W(t)在区间[25,30]单减,W(t)max=W(25)=13000,W(t)min=W(30)=12400;…(11分)
综上,当t=1时,W(t)最大值为20200;当t=10时,W(t)最小值为12100…(13分).
| 1 |
| t |
| 100 |
| t |
当25≤t≤30时,W(t)=g(t)f(t)=100(150-t)(1+
| 1 |
| t |
| 150 |
| t |
所以W(t)=
|
(2)(i)当1≤t<25时,由双勾函数的性质知W(t)=100(t+
| 100 |
| t |
因为W(10)=12100,W(1)=20200,W(25)=13000,
所以当t=10时,W(t)最小值为12100,当t=1时,W(t)最大值为20200;…(9分)
(ii)当25≤t≤30时,W(t)=100(
| 150 |
| t |
| 150 |
| t |
W(t)在区间[25,30]单减,W(t)max=W(25)=13000,W(t)min=W(30)=12400;…(11分)
综上,当t=1时,W(t)最大值为20200;当t=10时,W(t)最小值为12100…(13分).
点评:本题考查函数模型的运用,考查函数的最值,考查学生利用数学知识解决实际问题,确定函数模型是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是( )
| A、m∥α,n∥α,则m∥n |
| B、m∥n,m∥α,则n∥α |
| C、m⊥α,m⊥β,则α∥β |
| D、α⊥γ,β⊥γ,则α∥β |
直线
x+y-2=0与圆x2+y2=4相交所得的弦的长为( )
| 3 |
A、2
| ||
B、2
| ||
C、
| ||
D、
|
甲、乙两人同时从图书馆走向教室,甲一半路程步行,一半路程跑步;乙一半时间步行,一半时间跑步,若两人步行、跑步的速度一样,则先到教室的是( )
| A、甲 | B、乙 |
| C、甲、乙同时到达 | D、无法确定 |
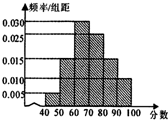 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为