题目内容

函数y=
3-x
+log2（x+2）的定义域为（　　）
A、（-∞，3]
B、（-2，3）
C、（-2，3]
D、（-∞，-2）∪[3，+∞）
考点：对数函数的定义域,函数的定义域及其求法
专题：函数的性质及应用
分析：根据根式函数和对数函数的性质即可求函数的定义域．
解答： 解：要使函数有意义，则
3-x≥0
x+2＞0
，
即
x≤3
x＞-2
，
解得-2＜x≤3，
∴函数的定义域为（-2，3]．
故选：C．
点评：本题主要考查函数定义域的求法，要求熟练掌握常见函数成立的条件，比较基础．
练习册系列答案
相关题目
假设小明家订了一份报纸，送报人可能在早上6：30至7：30之间把报纸送到小明家，小明爸爸离开家去工作的时间在早上7：00至8：00之间，问小明的爸爸在离开家前能得到报纸的概率是
 
．
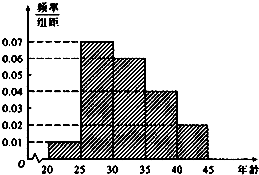某市为增强市民的环境保护意识，面向全市征召义务宣传志愿者．现从符合条件的志愿者中随机抽取100名按年龄分组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45]，得到的频率分布直方图如图所示．
（Ⅰ）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动，应从第3，4，5组各抽取多少名志愿者？
（Ⅱ） 在（1）的条件下，该市决定在第3，4组的志愿者中随机抽取2名志愿者介绍宣传经验，求第4组至少有一名志愿者被抽中的概率．
已知Sn为数列{an}的前n项和，Sn=λan-1（其中λ为常数）
（1）是否存在实数λ，使得数列{an}是等差数列？若存在，求出λ的值，若不存在，说明理由．
（2）当λ=2时，若数列{bn}满足bn+1=an+bn，且b1=
3
2
，令cn=2bn+n．求数列{cn}的前n项和Tn．
若向量
a
=(x-1，2)，
b
=(4，y)相互垂直，则点（2，3）到点（x，y）的距离的最小值为
 
．
直线x=1的倾斜角和斜率分别是（　　）
A、90°，不存在
B、45°，1
C、135°，-1
D、180°，不存在
已知f（x）=sinx+
3
cosx（x∈R）．求：
（1）若x∈R，求f（x）的值域，并写出f（x）的单调递增区间；
（2）若x∈(-
π
2
，
π
3
)，求f（x）的值域．
下列各函数中，是指数函数的是（　　）
A、y=（-3）x
B、y=-3x
C、y=3x-1
D、y=3x
设f(x)=
2-x
log81x
x∈(-∞，1]
x∈(1，+∞)
，则满足f(x)=
1
4
的x的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网