题目内容
已知函数f(x)=sin(ωx+
)ω(>0)的最小正周期为π
(1)求ω的值
(2)设α∈(0,
),β∈(
,π),f(
α+
)=
,f(
β+
)=-
,求sin(α+β)的值.
| π |
| 6 |
(1)求ω的值
(2)设α∈(0,
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
| 1 |
| 2 |
| 5π |
| 12 |
| 12 |
| 13 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:计算题
分析:(1)利用最小正周期为π,与ω>0,确定ω的值;
(2)利用f(
α+
)=
,f(
β+
)=-
,求sinα、sinβ的值,再根据角的范围求cosα、cosβ的值,然后利用公式sin(α+β)=sinαcosβ+cosαsinβ计算.
(2)利用f(
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
| 1 |
| 2 |
| 5π |
| 12 |
| 12 |
| 13 |
解答:
解:(1)函数f(x)=sin(ωx+
)的最小正周期为π,且ω>0
则2π=ω×π,
∴ω=2;
(2)由(1)得f(x)=sin(2x+
)
∴f(-
α+
)=sin[2(-
α+
)+
]=sin(
-α)=cosα=
.
∵α∈(0,
)
又f(
β+
)=sin[2(
β+
)+
]=sin(π+β)=-sinβ=-
,
∴sinβ=
,∵β∈(
,π),
∴cosβ=-
,
∴sin(α+β)=sinαcosβ+cosαsinβ=
×(-
)+
×
=
.
| π |
| 6 |
则2π=ω×π,
∴ω=2;
(2)由(1)得f(x)=sin(2x+
| π |
| 6 |
∴f(-
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 3 |
| 5 |
∵α∈(0,
| π |
| 2 |
又f(
| 1 |
| 2 |
| 5π |
| 12 |
| 1 |
| 2 |
| 5π |
| 12 |
| π |
| 6 |
| 12 |
| 13 |
∴sinβ=
| 12 |
| 13 |
| π |
| 2 |
∴cosβ=-
| 5 |
| 13 |
∴sin(α+β)=sinαcosβ+cosαsinβ=
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 12 |
| 13 |
| 16 |
| 65 |
点评:本题考查了三角函数的最小正周期,考查了两角和的正弦函数公式,要注意利用角的范围求角的三角函数值.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
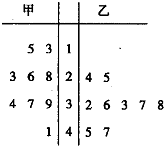 如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为
如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线
x+y-2=0与圆x2+y2=4相交所得的弦的长为( )
| 3 |
A、2
| ||
B、2
| ||
C、
| ||
D、
|