题目内容
已知关于x的不等式ax2+bx+c<0的解集为 {x|x<-1,或x>
},则关于x的不等式c(lgx)2+lgxb+a<0的解集为 .
| 1 |
| 2 |
考点:其他不等式的解法,一元二次不等式的解法
专题:函数的性质及应用
分析:由题意可得a<0,且
=-2,c>0,
=-1,则关于x的不等式即(lgx)2+
lgx+
<0,即 (lgx)2-lgx-2<0,解得lgx的范围,可得x的范围.
| a |
| c |
| b |
| c |
| b |
| c |
| a |
| c |
解答:
解:∵不等式ax2+bx+c<0的解集为 {x|x<-1,或x>
},
∴-1和
是ax2+bx+c=0的且a<0,
∴-1+
=-
,且-1×
=
,∴
=-2,c>0,
=-1.
则关于x的不等式c(lgx)2+lgxb+a<0,
即 (lgx)2+
lgx+
<0,即 (lgx)2-lgx-2<0,
解得-1<lgx<2,可得
<x<100,
故答案为:{x|
<x<100}.
| 1 |
| 2 |
∴-1和
| 1 |
| 2 |
∴-1+
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| c |
| a |
| a |
| c |
| b |
| c |
则关于x的不等式c(lgx)2+lgxb+a<0,
即 (lgx)2+
| b |
| c |
| a |
| c |
解得-1<lgx<2,可得
| 1 |
| 10 |
故答案为:{x|
| 1 |
| 10 |
点评:本题主要考查一元二次不等式的解法,韦达定理的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
下列各函数中,是指数函数的是( )
| A、y=(-3)x |
| B、y=-3x |
| C、y=3x-1 |
| D、y=3x |
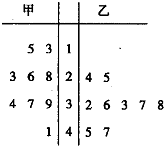 如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为
如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
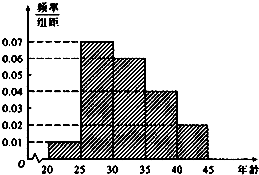 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.