题目内容
已知椭圆C的对称中心为原点O，焦点在x轴上，左右焦点分别为F1和F2，且|F1F2|=2，点（1，
）在该椭圆上．
（1）求椭圆C的方程；
（2）斜率为1且过F1的直线l与椭圆C相交于A，B两点，求|AB|．
| 3 |
| 2 |
（1）求椭圆C的方程；
（2）斜率为1且过F1的直线l与椭圆C相交于A，B两点，求|AB|．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）先设出椭圆的方程，根据题设中的焦距求得c和焦点坐标，根据点（1，
）到两焦点的距离求得a，进而求得b，得到椭圆的方程．
（2）直线l：y=x+1，代入椭圆方程3x2+4（x+1）2=12，设A（x1，y1），B（x2，y2），求出|x1-x2|，即可求弦MN的长．
| 3 |
| 2 |
（2）直线l：y=x+1，代入椭圆方程3x2+4（x+1）2=12，设A（x1，y1），B（x2，y2），求出|x1-x2|，即可求弦MN的长．
解答：
解：（1）设椭圆的方程为：
+
=1（a＞b＞0），
由题意可得：椭圆C两焦点坐标分别为F1（-1，0），F2（1，0）．
∴2a=
+
=4．
∴a=2，又c=1，b2=4-1=3，
故椭圆的方程为
+
=1．
（2）斜率为1且过F1的直线l的方程为：y=x+1，
代入椭圆方程3x2+4（x+1）2=12，
整理可得7x2+8x-8=0，
设A（x1，y1），B（x2，y2），则x1+x2=-
，x1x2=-
，
∴|x1-x2|=
=
，
∴|AB|=
•
=
．
| x2 |
| a2 |
| y2 |
| b2 |
由题意可得：椭圆C两焦点坐标分别为F1（-1，0），F2（1，0）．
∴2a=
(1+1)2+(
|
(1-1)2+(
|
∴a=2，又c=1，b2=4-1=3，
故椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）斜率为1且过F1的直线l的方程为：y=x+1，
代入椭圆方程3x2+4（x+1）2=12，
整理可得7x2+8x-8=0，
设A（x1，y1），B（x2，y2），则x1+x2=-
| 8 |
| 7 |
| 8 |
| 7 |
∴|x1-x2|=
|
12
| ||
| 7 |
∴|AB|=
| 2 |
12
| ||
| 7 |
| 24 |
| 7 |
点评：本题考查椭圆的方程与性质，考查直线与椭圆的位置关系，考查弦长的计算，考查学生的计算能力．考查了学生综合运用所学知识，创造性地解决问题的能力．
练习册系列答案
相关题目
设全集U=R，M={x|
＜2x＜1}，N={x|ln（-x）＞0}，则M∩∁UN=（ ）
| 1 |
| 8 |
| A、{x|x≥-1} |
| B、{x|-3＜x＜0} |
| C、{x|x≤-3} |
| D、{x|-1≤x＜0} |
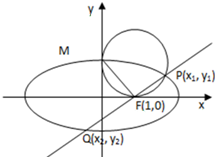椭圆G：
如图，已知焦点在x轴上的椭圆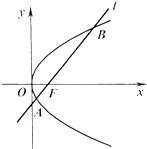
如图，已知抛物线C：y2=4x焦点为F，直线l经过点F且与抛物线C相交于A，B两点