题目内容
设全集U=R,M={x|
<2x<1},N={x|ln(-x)>0},则M∩∁UN=( )
| 1 |
| 8 |
| A、{x|x≥-1} |
| B、{x|-3<x<0} |
| C、{x|x≤-3} |
| D、{x|-1≤x<0} |
考点:交、并、补集的混合运算
专题:集合
分析:分别求出M与N中不等式的解集确定出M与N,根据全集U=R求出N的补集,找出M与N补集的交集即可.
解答:
解:由M中的不等式变形得:2-3<2x<20,即-3<x<0,
∴M={x|-3<x<0};
由N中的不等式变形得:ln(-x)>0=ln1,即-x>1,
解得:x<-1,即N={x|x<-1},
∵全集U=R,
∴∁UN={x|x≥-1},
则M∩∁UN={x|-1≤x<0}.
故选:D.
∴M={x|-3<x<0};
由N中的不等式变形得:ln(-x)>0=ln1,即-x>1,
解得:x<-1,即N={x|x<-1},
∵全集U=R,
∴∁UN={x|x≥-1},
则M∩∁UN={x|-1≤x<0}.
故选:D.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
下列选项一定正确的是( )
| A、若a>b,则ac>bc | ||||
B、若
| ||||
| C、若a2>b2,则a>b | ||||
D、若
|
若实数x,y满足不等式组
,则z=2x+3y的最大值是( )
|
| A、13 | B、12 | C、11 | D、10 |
如图所示的程序框图,能使输入的x值与输出的y值相等的x值个数为( )
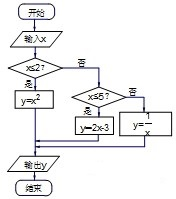

| A、1 | B、2 | C、3 | D、4 |