题目内容
已知等差数列{an}中,a3=9,a9=-3,a17= .
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:利用等差数列的通项公式求解.
解答:
解:∵等差数列{an}中,a3=9,a9=-3,
∴
,
解得a1=13,d=-2,
∴a17=13+16×(-2)=-19.
故答案为:-19.
∴
|
解得a1=13,d=-2,
∴a17=13+16×(-2)=-19.
故答案为:-19.
点评:本题考查等差数列的第17项的求法,是基础题,解题时要认真审题,注意等差数列的通项公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等比数列{an}中,S2=7,S6=91,则S4=( )
| A、28或-21 | B、28 |
| C、-21 | D、以上都不对 |
设f(x)=sin
,则f(1)+f(2)+f(3)+…+f(2010)=( )
| xπ |
| 3 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、1 |
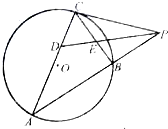 如图,PC是圆O的切线,切点为C,直线PA与圆O交于两点A、B,∠APC的平分线分别交弦CA、CB于两点D、E,已知PC=3,PB=2,则
如图,PC是圆O的切线,切点为C,直线PA与圆O交于两点A、B,∠APC的平分线分别交弦CA、CB于两点D、E,已知PC=3,PB=2,则