题目内容
若函数f（x）=x（|
|+|
|）是奇函数，则t的值为 ．
| x+2 |
| 3+t |
| x-7 |
| 3 |
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由题意知，f（-1）+f（1）=0，进而可知-1（|
|+|
|）+1（|
|+2）=0，解出即可．
| 1 |
| 3+t |
| -8 |
| 3 |
| 3 |
| 3+t |
解答：
解：∵函数f（x）=x（|
|+|
|）是奇函数，
∴f（-1）+f（1）=0，
即-1（|
|+|
|）+1（|
|+2）=0，
解得，t=0或t=-6．
故答案为：t=0或t=-6．
| x+2 |
| 3+t |
| x-7 |
| 3 |
∴f（-1）+f（1）=0，
即-1（|
| 1 |
| 3+t |
| -8 |
| 3 |
| 3 |
| 3+t |
解得，t=0或t=-6．
故答案为：t=0或t=-6．
点评：本题考查了函数的奇偶性应用于求参数，属于基础题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
若x，y满足约束条件
，则z=x-y的最小值是（ ）
|
| A、-3 | ||
| B、0 | ||
C、
| ||
| D、3 |
若集合A=[-1，1]，B={y|y=x2，x∈R}，则A∩B=（ ）
| A、{x|-1≤x≤1} |
| B、{x|x≥0} |
| C、{x|0≤x≤1} |
| D、∅ |
已知集合A={x∈R|x＞1}，B={x∈R|x2-x-2＜0}，则A∩B等于（ ）
| A、（-1，2） |
| B、（-1，+∞） |
| C、（-1，1） |
| D、（1，2） |
下列函数中与函数y=x是相同函数的是（ ）
A、y=(
| |||
B、y=
| |||
C、y=
| |||
D、y=
|
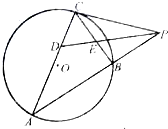如图，PC是圆O的切线，切点为C，直线PA与圆O交于两点A、B，∠APC的平分线分别交弦CA、CB于两点D、E，已知PC=3，PB=2，则