题目内容
1.若x,y满足:$\left\{\begin{array}{l}{x+2y-19≥0}\\{x-y+8≥0}\\{2x+y-14≤0}\end{array}\right.$,则z=$\frac{y+1}{x+1}$的最大值与最小值之和为( )| A. | $\frac{25}{4}$ | B. | $\frac{27}{4}$ | C. | $\frac{29}{4}$ | D. | $\frac{31}{4}$ |
分析 由约束条件作出可行域,再由z=$\frac{y+1}{x+1}$的几何意义,即可行域内的动点与定点P(-1,-1)连线的斜率求解.
解答 解:由约束条件$\left\{\begin{array}{l}{x+2y-19≥0}\\{x-y+8≥0}\\{2x+y-14≤0}\end{array}\right.$作出可行域如图,
z=$\frac{y+1}{x+1}$的几何意义为可行域内的动点与定点P(-1,-1)连线的斜率,
联立方程组求得A(1,9),C(3,8),
又${k}_{PA}=5,{k}_{PC}=\frac{9}{4}$,
∴z=$\frac{y+1}{x+1}$的最大值与最小值之和为$\frac{29}{4}$,
故选:C.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
12.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}x≥0\\ x+y≤2\\ x≤y\end{array}\right.$所表示的平面区域的面积为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
9.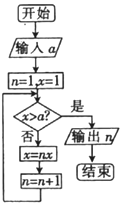 执行如图所示程序框图,若输出的结果为5,则输入的实数a的范围是( )
执行如图所示程序框图,若输出的结果为5,则输入的实数a的范围是( )
 执行如图所示程序框图,若输出的结果为5,则输入的实数a的范围是( )
执行如图所示程序框图,若输出的结果为5,则输入的实数a的范围是( )| A. | [6,24) | B. | [24,120) | C. | (-∞,6) | D. | (5,24) |
16.已知向量$\overrightarrow a=(cosθ,sinθ)$,向量$\overrightarrow{b}$=($\sqrt{3}$,1),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则tanθ的值是( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
6.为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房心理预测调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表:
已知样本中城市人数与农村人数之比是3:8.
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)从参与调研的城市人中用分层抽样方法抽取6人,进一步统计城市人的某项收入指标,假设一个买房人的指标算作3,一个纠结人的指标算作2,一个不买房人的指标算作1,现在从这6人中再随机选取3人,令X=再抽取3人指标之和,求X的分布列和数学期望.
| 买房 | 不买房 | 纠结 | |
| 城市人 | 5 | 15 | |
| 农村人 | 20 | 10 |
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)从参与调研的城市人中用分层抽样方法抽取6人,进一步统计城市人的某项收入指标,假设一个买房人的指标算作3,一个纠结人的指标算作2,一个不买房人的指标算作1,现在从这6人中再随机选取3人,令X=再抽取3人指标之和,求X的分布列和数学期望.
13.某象棋俱乐部有队员5人,其中女队员2人,现随机选派2人参加象棋比赛,则选出的2人中恰有1人是女队员的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
10.设x∈R,则“|x-2|<1”是“x2-2x-8<0”的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |