题目内容
已知双曲线
-
=1的左、右焦点为F1、F2，过F2的直线与双曲线右支相交于A、B两点，若|AF1|、|AB|、|BF2|依次成等差数列，则|AB|= ．
| x2 |
| a2 |
| y2 |
| b2 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由双曲线的定义有|BF1|-|BF2|=2a，|AF1|-|AF2|=2a，可得|BF1|=|BF2|+2a，|AF1|=|AF2|+2a，根据|AF1|、|AB|、|BF2|依次成等差数列，可得2AB=|AF1|+|BF2|，代入即可得出结论．
解答：
解：由双曲线的定义有|BF1|-|BF2|=2a，|AF1|-|AF2|=2a，
所以|BF1|=|BF2|+2a，|AF1|=|AF2|+2a，
又|AF1|、|AB|、|BF2|依次成等差数列，
所以2AB=|AF1|+|BF2|=|AF2|+2a+|BF2|+2a=|AB|+2a，
所以|AB|=2a．
故答案为：2a．
所以|BF1|=|BF2|+2a，|AF1|=|AF2|+2a，
又|AF1|、|AB|、|BF2|依次成等差数列，
所以2AB=|AF1|+|BF2|=|AF2|+2a+|BF2|+2a=|AB|+2a，
所以|AB|=2a．
故答案为：2a．
点评：本题考查等差数列的性质，考查双曲线的定义，考查学生分析解决问题的能力，正确运用双曲线的定义是关键．
练习册系列答案
相关题目
如图，在四棱锥S-ABCD中，底面ABCD是正方形，四个侧面都是等边三角形，AC与BD的交点为O，E为侧棱SC的中点．
如图，正方形ABCD与梯形CDEF所在的平面互相垂直，CD⊥DE，CF∥DE，CD=CF=2，DE=4，G为AE的中点．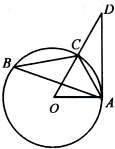
如图，已知△ABC内接于圆O，点D在OC的延长线上，AD是圆O的切线，若∠OAC=60°，AC=1，则AD的长为