题目内容
若双曲线
-
=1(a>0,b>0)与抛物线y2=
bx有一个公共交点为(3,
),则此双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件,利用待定系数法求出双曲线方程,由此能求出双曲线的离心率.
解答:
解:∵双曲线
-
=1(a>0,b>0)与抛物线y2=
bx有一个公共交点为(3,
),
∴
,解得a=
,b=1,c=2,
∴e=
=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 2 |
∴
|
| 3 |
∴e=
| c |
| a |
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查双曲线的离心率的求法,是基础题,解题时要熟练掌握双曲线抛物线的性质.

练习册系列答案
相关题目
设函数f(x)=sin(ωx+
)(ω>0)的最小正周期为π,则f(x)( )
| π |
| 2 |
A、在(0,
| ||||
B、在(
| ||||
C、在(0,
| ||||
D、在(
|
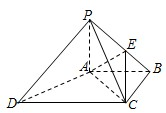 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB. 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2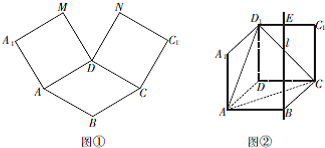 如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).
如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).