题目内容
 如图,正方形ABCD与梯形CDEF所在的平面互相垂直,CD⊥DE,CF∥DE,CD=CF=2,DE=4,G为AE的中点.
如图,正方形ABCD与梯形CDEF所在的平面互相垂直,CD⊥DE,CF∥DE,CD=CF=2,DE=4,G为AE的中点.(Ⅰ)求证:FG∥平面ABCD;
(Ⅱ)求证:平面FAD⊥平面FAE;
(Ⅲ)求平面FAE与平面ABCD所成锐二面角的余弦值.
考点:用空间向量求平面间的夹角,平面与平面垂直的判定,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(I)取DA中点N,连接GN,CN,由三角形中位线定理,结合已知中CF∥DE,CF=2,DE=4,易得四边形GFCN为平行四边形,所以FG∥CN,再由线面平面的判定定理,可得FG∥平面ABCD;
(II)由已知中正方形ABCD与梯形CDEF所在的平面互相垂直,易得AD⊥平面CDEF,进而AD⊥EF,再证明EF⊥DF,由线面垂直的判定定理可得EF⊥平面ADF,再由面面垂直的判定定理,即可得到平面FAD⊥平面FAE;
(III)以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系,分别求出平面FAE与平面ABCD的法向量,代入向量夹角公式,即可求出平面FAE与平面ABCD所成锐二面角的余弦值.
(II)由已知中正方形ABCD与梯形CDEF所在的平面互相垂直,易得AD⊥平面CDEF,进而AD⊥EF,再证明EF⊥DF,由线面垂直的判定定理可得EF⊥平面ADF,再由面面垂直的判定定理,即可得到平面FAD⊥平面FAE;
(III)以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系,分别求出平面FAE与平面ABCD的法向量,代入向量夹角公式,即可求出平面FAE与平面ABCD所成锐二面角的余弦值.
解答:
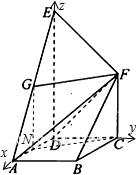 (I)证明:取DA中点N,连接GN,CN
(I)证明:取DA中点N,连接GN,CN
在△EAB中,G、N分别为EA,AD的中点,
∴GN∥EB,且GN=
EB.
由已知CF∥DE,CF=2,DE=4,
∴CF∥EB,且CF=
EB.
∴CF∥GN且CF=GN,
∴四边形GFCN为平行四边形,
∴FG∥CN,
∵CN?平面ABCD,且FG?平面ABCD,
∴FG∥平面ABCD;
(II)证明:在正方形ADEF中,AD⊥CD,
又∵平面CDEF⊥平面ABCD,且平面CDEF∩平面ABCD=CD,
∴AD⊥平面CDEF,
∴AD⊥EF.
在直角梯形CDEF中,CD=CF=2,DE=4,可得DF=2
在△DEF中,EF=DF=2
,DE=4,
∴EF⊥DF.
∵AD∩DF=D
∴EF⊥平面ADF,
∵EF?平面AEF,
∴平面FAD⊥平面FAE;
(Ⅲ)解:以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系.
则平面ABCD的一个法向量为
=(0,0,4).
设平面FAE的一个法向量为
=(x,y,z),则
∵
=(0,2,2),
=(2,0,0),
∴
,
∴可取
=(0,1,-1).
设平面BEC与平面ADEF所成锐二面角为θ,
则cosθ=|
|=
,
∴平面FAE与平面ABCD所成锐二面角的余弦值为
.
 (I)证明:取DA中点N,连接GN,CN
(I)证明:取DA中点N,连接GN,CN在△EAB中,G、N分别为EA,AD的中点,
∴GN∥EB,且GN=
| 1 |
| 2 |
由已知CF∥DE,CF=2,DE=4,
∴CF∥EB,且CF=
| 1 |
| 2 |
∴CF∥GN且CF=GN,
∴四边形GFCN为平行四边形,
∴FG∥CN,
∵CN?平面ABCD,且FG?平面ABCD,
∴FG∥平面ABCD;
(II)证明:在正方形ADEF中,AD⊥CD,
又∵平面CDEF⊥平面ABCD,且平面CDEF∩平面ABCD=CD,
∴AD⊥平面CDEF,
∴AD⊥EF.
在直角梯形CDEF中,CD=CF=2,DE=4,可得DF=2
| 2 |
在△DEF中,EF=DF=2
| 2 |
∴EF⊥DF.
∵AD∩DF=D
∴EF⊥平面ADF,
∵EF?平面AEF,
∴平面FAD⊥平面FAE;
(Ⅲ)解:以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系.
则平面ABCD的一个法向量为
| m |
设平面FAE的一个法向量为
| n |
∵
| DF |
| DA |
∴
|
∴可取
| n |
设平面BEC与平面ADEF所成锐二面角为θ,
则cosθ=|
| ||||
|
|
| ||
| 2 |
∴平面FAE与平面ABCD所成锐二面角的余弦值为
| ||
| 2 |
点评:本题考查二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定,熟练掌握空间直线与平面不同位置关系(平行和垂直)的判定定理、性质定理、定义及几何特征是解答本题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD. 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2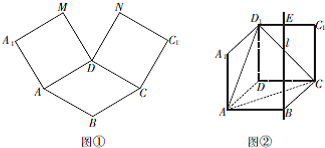 如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).
如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).