题目内容
6.计算椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1所围成的平面图形的面积A.分析 因为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1关于x轴和y轴都是对称的,所以所求之面积为s=4${∫}_{0}^{a}$$\frac{a}{b}\sqrt{{a}^{2}-{x}^{2}}$dx,利用换元法,即可得出结论.
解答 解:因为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1关于x轴和y轴都是对称的,
所以所求之面积为s=4${∫}_{0}^{a}$$\frac{a}{b}\sqrt{{a}^{2}-{x}^{2}}$dx
令x=asinθ.(0≤θ≤$\frac{π}{2}$)
则s=4${∫}_{0}^{\frac{π}{2}}$$\frac{b}{a}$•a•cosθ•a•cosθdθ=4ab${∫}_{0}^{\frac{π}{2}}$(cosθ)2dθ=4ab${∫}_{0}^{\frac{π}{2}}$$\frac{1+cos2θ}{2}$dθ
=2ab[$\frac{π}{2}$+${∫}_{0}^{\frac{π}{2}}$cos2θdθ]=2ab•$\frac{π}{2}$=πab.
点评 本题考查利用定积分求面积,考查换元方法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
14.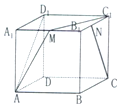 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )
 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
11.函数$f(x)=3sin(2x+\frac{π}{2})$是( )
| A. | 周期为$\frac{π}{2}$的奇函数 | B. | 周期为$\frac{π}{2}$的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的偶函数 |
18.已知$f(x)=\frac{x}{{{2^x}-1}},g(x)=\frac{x}{2}$,则下列结论正确的是( )
| A. | h(x)=f(x)+g(x)是偶函数 | B. | h(x)=f(x)+g(x)是奇函数 | ||
| C. | h(x)=f(x)g(x)是奇函数 | D. | h(x)=f(x)g(x)是偶函数 |
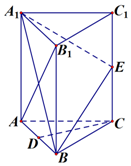 如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点. 如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.