Question

14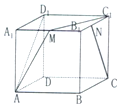．在棱长为1的正方体ABCD-A₁B₁C₁D₁中，M和N分别为A₁B₁和B₁C₁的中点，那么直线AM与CN所成角的余弦值是（　　）

• A． $\frac{{\sqrt{3}}}{2}$
• B． $\frac{{\sqrt{10}}}{10}$
• C． $\frac{3}{5}$
• D． $\frac{4}{5}$

Answer 1

分析 取AB中点E，BC中点F，连接B₁E，B₁F，则∠EB₁F为直线AM与CN所成角，设正方体棱长为2a，然后利用余弦定理求解．

解答 解：如图，取AB中点E，BC中点F，连接B₁E，B₁F，
则四边形AEB₁M，B₁FCN为平行四边形，
∴AM∥B₁E，CN∥B₁F，
∴∠EB₁F为直线AM与CN所成角（或补角），
正方体的棱长为1，则BE=BF=$\frac{1}{2}$，EF=$\frac{\sqrt{2}}{2}$，B₁F=B₁E=$\frac{\sqrt{5}}{2}a$，
∴cos∠EB₁F=$\frac{4}{5}$．
∴直线AM与CN所成角的余弦值是$\frac{4}{5}$．
故选：D．

点评 本题考查异面直线所成的角，关键是找出角，是中档题．