题目内容
16. 如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.(1)求证:M是PC的中点;
(2)在PA上是否存在点F,使二面角F-BD-M为直角?若存在,求出$\frac{AF}{AP}$的值;若不存在,说明理由.
分析 (1)连AC交BD于E,连ME,推导出E是AC中点,PA∥ME,由此能证明M是PC的中点.
(2)取AD中点O,以O为原点,OA,OE,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法求出存在F,使二面角F-BD-M为直角,此时$\frac{AF}{AP}=\frac{3}{8}$.
解答 证明:(1)连AC交BD于E,连ME.
∵ABCD是矩形,∴E是AC中点.
又PA∥面MBD,且ME是面PAC与面MDB的交线,
∴PA∥ME,∴M是PC的中点.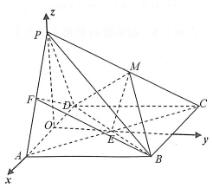
解:(2)取AD中点O,由(1)知OA,OE,OP两两垂直.
以O为原点,OA,OE,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系(如图),
则各点坐标为$A({1,0,0}),B({1,3,0}),D({-1,0,0}),C({-1,3,0}),P({0,0,\sqrt{3}}),M({-\frac{1}{2},\frac{3}{2},\frac{{\sqrt{3}}}{2}})$.
设存在F满足要求,且$\frac{AF}{AP}=λ$,
则由$\overrightarrow{AF}=λ\overrightarrow{AP}$得:$F({1-λ,0,\sqrt{3}λ})$,
面MBD的一个法向量为$\overrightarrow n=({1,-\frac{2}{3},\frac{{\sqrt{3}}}{3}})$,
面FBD的一个法向量为$\overrightarrow m=({1,-\frac{2}{3},\frac{λ-2}{{\sqrt{3}λ}}})$,
由$\overrightarrow n•\overrightarrow m=0$,得$1+\frac{4}{9}+\frac{λ-2}{3λ}=0$,解得$λ=\frac{3}{8}$,
故存在F,使二面角F-BD-M为直角,此时$\frac{AF}{AP}=\frac{3}{8}$.
点评 本题考查点是线段的中点的证明,考查满足条件的点的位置的确定与线段比值的求法,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、转化化归思想,是中档题.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案| 父亲身高x/cm | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y/cm | 175 | 176 | 177 | 178 | 179 |
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=x+1 | C. | $\widehat{y}$=88+$\frac{1}{2}$x | D. | $\widehat{y}$=176 |
| A. | 有最小值 $\frac{{11+2\sqrt{10}}}{3}$ | B. | 有最大值$\frac{{11+2\sqrt{10}}}{3}$ | ||
| C. | 有最小值$\frac{{11-2\sqrt{10}}}{3}$ | D. | 有最大值$\frac{{11-2\sqrt{10}}}{3}$ |
| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0} | D. | {-2,1,2} |
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
| 天津 | 24 | 22 | 26 | 23 | 24 | 26 | 27 | 25 | 28 | 24 | 25 | 26 |
| 上海 | 32 | 27 | 33 | 31 | 30 | 31 | 32 | 33 | 30 | 32 | 30 | 30 |

(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;
(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;
(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设X为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出X的数学期望(不需要计算过程).