题目内容
求下列数列的通项公式,Sn是其前n项和.
(1)Sn=2n2-3n-1;
(2)Sn=3n-2n+1.
(1)Sn=2n2-3n-1;
(2)Sn=3n-2n+1.
考点:数列的求和
专题:等差数列与等比数列
分析:首先根据Sn=2n2-3n-1求出a1的值,然后利用an=Sn-Sn-1求出当n≥2时,an的表达式,然后验证a1的值,最后写出an的通项公式
解答:
解:(1)n=1时,a1=s1=2-3-1=-2,
n≥2时,an=Sn-Sn-1=(2n2-3n-1)-[2(n-1)2-3(n-1)-1]=4n-5,
经检验当n=1时,4n-5=-1≠-2,
∴an=
.
(2)n=1时,a1=s1=3-2+1=2,
n≥2时,an=Sn-Sn-1=3n-2n+1-[3n-1-2(n-1)+1]=2×3n-1-2,
经检验当n=1时,2×3n-1-2=0≠2,
∴an=
.
n≥2时,an=Sn-Sn-1=(2n2-3n-1)-[2(n-1)2-3(n-1)-1]=4n-5,
经检验当n=1时,4n-5=-1≠-2,
∴an=
|
(2)n=1时,a1=s1=3-2+1=2,
n≥2时,an=Sn-Sn-1=3n-2n+1-[3n-1-2(n-1)+1]=2×3n-1-2,
经检验当n=1时,2×3n-1-2=0≠2,
∴an=
|
点评:本题主要考查数列递推式的知识点,解答本题的关键是利用an=Sn-Sn-1(n≥2)进行解答,此题难度不大,很容易进行解答.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
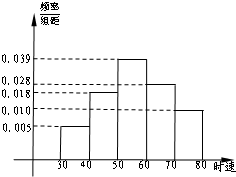 5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )
5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )| A、50 | B、500 |
| C、1000 | D、4500 |
设向量
=(x,0),
=(x-2,1),集合A={x|
•
≥0},B={x|0<x<4},则A∩B=( )
| a |
| b |
| a |
| b |
| A、[2,4) |
| B、(2,4) |
| C、(-∞,4) |
| D、(-∞,0] |
若复数z满足:z+1=
(1+i),其中
是复数z的共轭复数,则z•
等于( )
. |
| z |
. |
| z |
. |
| z |
| A、3 | B、5 | C、8 | D、10 |