题目内容
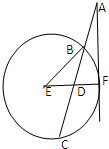 如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=
如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=| 1 |
| 3 |
(1)求AF的长;
(2)求证:AD=3ED.
考点:与圆有关的比例线段
专题:直线与圆
分析:(1)延长BE交圆E于点M,连结CM,则∠BCM=90°,由已知条件求出AB,AC,再由切割线定理能求出AF.
(2)过E作EH⊥BC于H,得到EDH∽△ADF,由此入手能够证明AD=3ED.
(2)过E作EH⊥BC于H,得到EDH∽△ADF,由此入手能够证明AD=3ED.
解答:
(1)解:延长BE交圆E于点M,连结CM,则∠BCM=90°,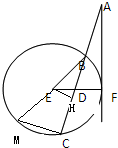
∵BM=2BE=4,∠EBC=30°,∴BC=2
,
又∵AB=
AC,∴AB=
BC=
,∴AC=3
,
根据切割线定理得AF2=AB•AC=
×3
=9,即AF=3
(2)证明:过E作EH⊥BC于H,
∵∠EOH=∠ADF,∠EHD=∠AFD,
∴△EDH∽△ADF,
∴
=
,
又由题意知CH=
BC=
,EB=2,
∴EH=1,∴
=
,
∴AD=3ED.

∵BM=2BE=4,∠EBC=30°,∴BC=2
| 3 |
又∵AB=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
根据切割线定理得AF2=AB•AC=
| 3 |
| 3 |
(2)证明:过E作EH⊥BC于H,
∵∠EOH=∠ADF,∠EHD=∠AFD,
∴△EDH∽△ADF,
∴
| ED |
| AD |
| EH |
| AF |
又由题意知CH=
| 1 |
| 2 |
| 3 |
∴EH=1,∴
| ED |
| AD |
| 1 |
| 3 |
∴AD=3ED.
点评:本题考查与圆有关的线段的求法,考查两条线段间数量关系的证明,是中档题,解题时要注意切割线定理的合理运用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
对于函数f(x)=cos2(x-
)+sin2(x+
)-1,下列选项中正确的是( )
| π |
| 12 |
| π |
| 12 |
A、f(x)在(
| ||||
| B、f(x)的图象关于原点对称 | ||||
| C、f(x)的最小正周期为2π | ||||
| D、f(x)的最大值为1 |
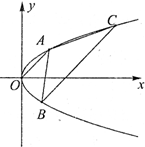 已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.
已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1. 在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.
在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.