题目内容
 在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.
在学习完统计学知识后,两位同学对所在年级的1200名同学一次数学考试成绩作抽样调查,两位同学采用简单随机抽样方法抽取100名学生的成绩,并将所选的数学成绩制成如下统计表,设本次考试的最低期望分数为90分,优等生最低分130分,并且考试成绩分数在[85,90)的学生通过自身努力能达到最低期望分数.(Ⅰ)求出各分数段的频率并作出频率分布直方图;
(Ⅱ)用所抽学生的成绩在各个分数段的频率表示概率,请估计该校学生数学成绩达到最低期望的学生分数和优等生人数;
(Ⅲ)设考试成绩在[85,90)的学生成绩如下:80,81,83,84,86,89,从分数在[85,90)的学生中抽取2人出来检查数学知识的掌握情况,求恰好有1名学生通过自身努力达到最低期望分数的概率.
| 分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 9 | 6 | 12 | 18 | 21 | 16 | 12 | 6 |
| 频率 |
考点:离散型随机变量的期望与方差,频率分布直方图
专题:计算题,概率与统计
分析:(Ⅰ)利用各分数段的人数除以100,可得各分数段的频率,从而可得频率分布直方图;
(Ⅱ)由(Ⅰ)可知达到最低期望的频率为0.85,优等生的频率为0.18,从而可求该校学生数学成绩达到最低期望的学生分数和优等生人数;
(Ⅲ)求出从分数在[85,90)的学生中抽取2人出来检查数学知识的掌握情况,选出2人,共有
=15种情况,恰好有1名学生通过自身努力的学生的人数,即可求恰好有1名学生通过自身努力达到最低期望分数的概率.
(Ⅱ)由(Ⅰ)可知达到最低期望的频率为0.85,优等生的频率为0.18,从而可求该校学生数学成绩达到最低期望的学生分数和优等生人数;
(Ⅲ)求出从分数在[85,90)的学生中抽取2人出来检查数学知识的掌握情况,选出2人,共有
| C | 2 6 |
解答:
解:(Ⅰ)利用各分数段的人数除以100,可得各分数段的频率.
频率分布直方图,如图所示
 ;
;
(Ⅱ)由(Ⅰ)可知达到最低期望的频率为0.85,优等生的频率为0.18,
∴最低期望的学生为1200×0.85=1020,优等生人数为1200×0.18=216;
(Ⅲ)从分数在[85,90)的学生中抽取2人出来检查数学知识的掌握情况,选出2人,共有
=15种情况,恰好有1名学生通过自身努力的学生有(80,86)(80,89),(81,86),(81,89),(83,86),(83,89),(84,86),(84,89),共8种情况,
∴恰好有1名学生通过自身努力达到最低期望分数的概率为
.
| 分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 9 | 6 | 12 | 18 | 21 | 16 | 12 | 6 |
| 频率 | 0.09 | 0.06 | 0.12 | 0.18 | 0.21 | 0.16 | 0.12 | 0.06 |
 ;
;(Ⅱ)由(Ⅰ)可知达到最低期望的频率为0.85,优等生的频率为0.18,
∴最低期望的学生为1200×0.85=1020,优等生人数为1200×0.18=216;
(Ⅲ)从分数在[85,90)的学生中抽取2人出来检查数学知识的掌握情况,选出2人,共有
| C | 2 6 |
∴恰好有1名学生通过自身努力达到最低期望分数的概率为
| 8 |
| 15 |
点评:本题考查频率分布直方图,考查概率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
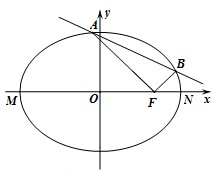 已知椭圆
已知椭圆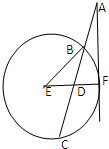 如图,过圆E外一点A作一条直线与圆E交于B,C两点,且
如图,过圆E外一点A作一条直线与圆E交于B,C两点,且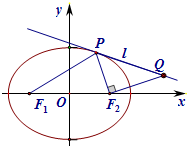 在平面直角坐标系xoy中,已知F1,F2分别是椭圆G:
在平面直角坐标系xoy中,已知F1,F2分别是椭圆G: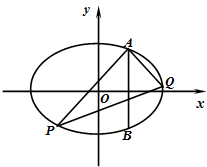 如图,两条相交线段AB、PQ的四个端点都在椭圆
如图,两条相交线段AB、PQ的四个端点都在椭圆 如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题:
如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题: