题目内容
设函数f(x)=
-2ax+3lnx.(0<a<3)
(1)当a=2时,求函数f(x)=
-2ax+3lnx的单调区间.
(2)当x∈[1,+∞)时,若f(x)≥-5xlnx+3lnx-
恒成立,求a的取值范围.
| x2 |
| 2 |
(1)当a=2时,求函数f(x)=
| x2 |
| 2 |
(2)当x∈[1,+∞)时,若f(x)≥-5xlnx+3lnx-
| 3 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求导数,利用导数的正负,可得函数f(x)=
-2ax+3lnx的单调区间.
(2)分离参数,可得
+
+
≥a,构造函数g(x)=
+
+
,证明g(x)在x∈[1,+∞)上为增函数,即可得出结论.
| x2 |
| 2 |
(2)分离参数,可得
| x |
| 4 |
| 5lnx |
| 2 |
| 3 |
| 4x |
| x |
| 4 |
| 5lnx |
| 2 |
| 3 |
| 4x |
解答:
解:(1)函数f(x)的定义域为(0,+∞),
当a=2时,f′(x)=
,
当x∈(0,1]时,f′(x)>0,f(x)为增函数.
当x∈(1,3]时,f′(x)<0,f(x)为减函数.
当x∈(3,+∞)时,f′(x)>0,f(x)为增函数.
∴函数f(x)单调增区间为(0,1],(3,+∞),单调减区间为(1,3];
(2)∵f(x)≥-5xlnx+3lnx-
,
∴
-2ax+5xlnx+
≥0,
∵x∈[1,+∞),
∴
+5xlnx+
≥2ax,
∴
+
+
≥a,
令g(x)=
+
+
,则g′(x)=
,
∵x∈[1,+∞),
∴x2+10x-3>0,
∴x∈[1,+∞)时,g′(x)>0,
∴g(x)在x∈[1,+∞)上为增函数,
∴g(x)≥g(1)
+
=1≥a,
∴0<a≤1.
当a=2时,f′(x)=
| (x-3)(x-1) |
| x |
当x∈(0,1]时,f′(x)>0,f(x)为增函数.
当x∈(1,3]时,f′(x)<0,f(x)为减函数.
当x∈(3,+∞)时,f′(x)>0,f(x)为增函数.
∴函数f(x)单调增区间为(0,1],(3,+∞),单调减区间为(1,3];
(2)∵f(x)≥-5xlnx+3lnx-
| 3 |
| 2 |
∴
| x2 |
| 2 |
| 3 |
| 2 |
∵x∈[1,+∞),
∴
| x2 |
| 2 |
| 3 |
| 2 |
∴
| x |
| 4 |
| 5lnx |
| 2 |
| 3 |
| 4x |
令g(x)=
| x |
| 4 |
| 5lnx |
| 2 |
| 3 |
| 4x |
| x2+10x-3 |
| 4x2 |
∵x∈[1,+∞),
∴x2+10x-3>0,
∴x∈[1,+∞)时,g′(x)>0,
∴g(x)在x∈[1,+∞)上为增函数,
∴g(x)≥g(1)
| 1 |
| 4 |
| 3 |
| 4 |
∴0<a≤1.
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查学生分析解决问题的能力,确定函数的单调性是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
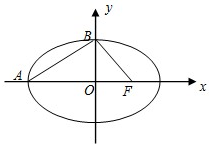 已知椭圆C:
已知椭圆C: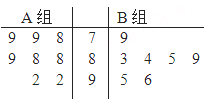 天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.
天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.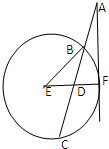 如图,过圆E外一点A作一条直线与圆E交于B,C两点,且
如图,过圆E外一点A作一条直线与圆E交于B,C两点,且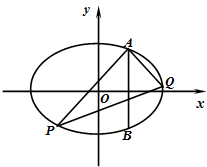 如图,两条相交线段AB、PQ的四个端点都在椭圆
如图,两条相交线段AB、PQ的四个端点都在椭圆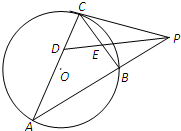 如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则
如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则