题目内容
对于函数f(x)=cos2(x-
)+sin2(x+
)-1,下列选项中正确的是( )
| π |
| 12 |
| π |
| 12 |
A、f(x)在(
| ||||
| B、f(x)的图象关于原点对称 | ||||
| C、f(x)的最小正周期为2π | ||||
| D、f(x)的最大值为1 |
考点:二倍角的余弦,两角和与差的正弦函数,二倍角的正弦,三角函数的周期性及其求法,正弦函数的单调性,正弦函数的对称性
专题:三角函数的图像与性质
分析:函数f(x)解析式前两项利用二倍角的余弦函数公式化简,整理后得到一个角的正弦函数,利用正弦函数的单调性,对称性,周期性,以及值域,即可做出判断.
解答:
解:函数f(x)=
[1+cos(2x-
)+1-cos(2x+
)]-1
=
(
cos2x+
sin2x-
cos2x+
sin2x)
=
sin2x,
令-
+2kπ≤2x≤
+2kπ,k∈Z,得到-
+kπ≤x≤
+kπ,k∈Z,
∴f(x)的递增区间为[-
+kπ,
+kπ],k∈Z,
当x∈(
,
)时,2x∈(
,π),此时函数为减函数,选项A错误;
当x=0时,f(x)=0,且正弦函数关于原点对称,选项B正确;
∵ω=2,∴最小正周期T=
=π,选项C错误;
∵-1≤sin2x≤1,
∴f(x)=
sin2x的最大值为
,选项D错误,
故选:B.
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
令-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
∴f(x)的递增区间为[-
| π |
| 4 |
| π |
| 4 |
当x∈(
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
当x=0时,f(x)=0,且正弦函数关于原点对称,选项B正确;
∵ω=2,∴最小正周期T=
| 2π |
| 3 |
∵-1≤sin2x≤1,
∴f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:此题考查了二倍角的余弦函数公式,两角和与差的正弦函数公式,三角函数的周期性及其求法,正弦函数的单调性,以及正弦函数的对称性,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
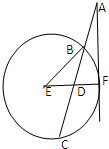 如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=
如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=| 1 |
| 3 |
(1)求AF的长;
(2)求证:AD=3ED.
已知函数f(x)是奇函数,且x∈(0,2)时,f(x)=2x,则f(-1)=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
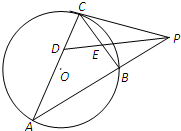 如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则
如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则 如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题:
如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题: