题目内容
已知t=(
)x+(
)x+(
)x,当(t-1)(t-2)(t-3)=0时,求所有实数解的和.
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
考点:指数型复合函数的性质及应用
专题:函数的性质及应用
分析:令f(x)=(
)x+(
)x+(
)x,则f(0)=3,f(1)=2,f(3)=1,若(t-1)(t-2)(t-3)=0,则x=0,或x=1,或x=3,进而得到答案.
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
解答:
解:令f(x)=(
)x+(
)x+(
)x,
则f(x)是减函数,
因此对任意正实数t,f(x)=t恰有惟一解,
当(t-1)(t-2)(t-3)=0时,
t=1,或t=2,或t=3,
又∵f(0)=3,f(1)=2,f(3)=1,
即方程(t-1)(t-2)(t-3)=0的所有解为0,1,3,
∴它们的和为4.
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
则f(x)是减函数,
因此对任意正实数t,f(x)=t恰有惟一解,
当(t-1)(t-2)(t-3)=0时,
t=1,或t=2,或t=3,
又∵f(0)=3,f(1)=2,f(3)=1,
即方程(t-1)(t-2)(t-3)=0的所有解为0,1,3,
∴它们的和为4.
点评:本题考查的知识点是指数函数的图象和性质,方程的根,其中分析出f(x)=(
)x+(
)x+(
)x的单调性,进而求出f(0)=3,f(1)=2,f(3)=1,是解答的关键.
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |

练习册系列答案
相关题目
给出下列语句:
①二次函数是偶函数吗?
②2>2;
③sin
=1;
④x2-4x+4=0.
其中是命题的有( )
①二次函数是偶函数吗?
②2>2;
③sin
| π |
| 2 |
④x2-4x+4=0.
其中是命题的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
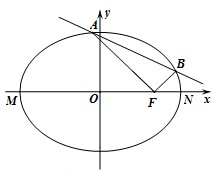 已知椭圆
已知椭圆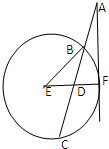 如图,过圆E外一点A作一条直线与圆E交于B,C两点,且
如图,过圆E外一点A作一条直线与圆E交于B,C两点,且