题目内容
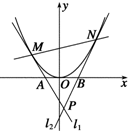 设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若AB=1,求点P的轨迹方程.
设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若AB=1,求点P的轨迹方程.考点:轨迹方程
专题:导数的综合应用,圆锥曲线的定义、性质与方程
分析:设P(x,y),M(x1,x12),N(x2,x22),由导数求得两直线的斜率,用点斜式求得 l1 的方程,同理求得l2 的方程,由此建立x,y 的方程.
解答:
解:设P(x,y),M(x1,x12),N(x2,x22),
由y=x2,得y′=2x,∴y′|x=x1=2x1,
∴l1 的方程为 y-x12=2x1(x-x1),即y=2x1x-x12 ①,
同理,l2 的方程为 y=2x2x-x22 ②,
令y=0,可求出 A(
,0),B(
,0).
∵|AB|=1,∴|x1-x2|=2,即|x1+x2|2-4x1x2 =4,
由①,②,得x=
,y=x1x2,
故点P(
,x1x2).
∴点P的轨迹方程为:y=x2-1,
由y=x2,得y′=2x,∴y′|x=x1=2x1,
∴l1 的方程为 y-x12=2x1(x-x1),即y=2x1x-x12 ①,
同理,l2 的方程为 y=2x2x-x22 ②,
令y=0,可求出 A(
| x1 |
| 2 |
| x2 |
| 2 |
∵|AB|=1,∴|x1-x2|=2,即|x1+x2|2-4x1x2 =4,
由①,②,得x=
| x1+x2 |
| 2 |
故点P(
| x1+x2 |
| 2 |
∴点P的轨迹方程为:y=x2-1,
点评:本题考查了轨迹方程的求法,考查了利用导数研究过曲线上某点处的切线方程,体现了整体运算思想方法,是中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知映射f:P(m,n)→P′(
,
)(m≥0,n≥0).设点A(1,3),B(2,2),点M是线段AB上一动点,f:M→M′.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点M′所经过的路线长度为( )
| m |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=log2(x+a)+log2(x-a)(a∈R).命题p:?a∈R,函数f(x)是偶函数;命题q:?a∈R,函数f(x)在定义域内是增函数.那么下列命题为真命题的是( )
| A、?q | B、p∧q |
| C、(?p)∧q | D、p∧(?q) |