题目内容
 函数f(x)=cos(πx+φ)(0<φ<
函数f(x)=cos(πx+φ)(0<φ<| π |
| 2 |
(Ⅰ)写出φ及图中x0的值;
(Ⅱ)求f(x)在区间[-
| 1 |
| 2 |
| 1 |
| 3 |
考点:余弦函数的图象,余弦函数的定义域和值域
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)由图观察可知,函数的图象过点(0,
),有
=cosφ可解得φ的值是
.由图观察可知,函数的图象过点(x0,
),有π×x0+
=2π-
,可解得x0的值.
(Ⅱ)由(Ⅰ)可知:f(x)=cos(πx+
).根据余弦函数的单调性即可求f(x)在区间[-
,
]上的最大值和最小值.
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
(Ⅱ)由(Ⅰ)可知:f(x)=cos(πx+
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:(Ⅰ)∵由图观察可知,函数的图象过点(0,
),
∴
=cosφ,
∵0<φ<
,
∴可解得φ的值是
.
∵由图观察可知,函数的图象过点(x0,
),
∴
=cos(π×x0+
)
∴π×x0+
=2π-
∴可解得x0的值是
.
(Ⅱ)由(Ⅰ)可知:f(x)=cos(πx+
).
因为x∈[-
,
],
所以-
≤πx+
≤
.
所以 当πx+
=0,即x=-
时f(x)取得最大值1;
当πx+
=
,即x=
时f(x)取得最小值-
.
| 1 |
| 2 |
∴
| 1 |
| 2 |
∵0<φ<
| π |
| 2 |
∴可解得φ的值是
| π |
| 3 |
∵由图观察可知,函数的图象过点(x0,
| 1 |
| 2 |
∴
| 1 |
| 2 |
| π |
| 3 |
∴π×x0+
| π |
| 3 |
| π |
| 3 |
∴可解得x0的值是
| 4 |
| 3 |
(Ⅱ)由(Ⅰ)可知:f(x)=cos(πx+
| π |
| 3 |
因为x∈[-
| 1 |
| 2 |
| 1 |
| 3 |
所以-
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
所以 当πx+
| π |
| 3 |
| 1 |
| 3 |
当πx+
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题主要考查了三角函数解析式的求法,余弦函数的定义域和值域,余弦函数的图象和性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
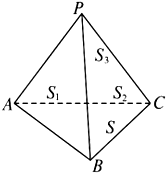 在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为
在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为 从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.
从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.