题目内容
已知函数f(x)=|x2-1|+x.
(1)画出图象;
(2)写出它的单调区间;
(3)当x∈{-3,
}时,求函数y=f(x)的最大值和最小值.
(1)画出图象;
(2)写出它的单调区间;
(3)当x∈{-3,
| 3 |
| 2 |
考点:带绝对值的函数
专题:计算题,作图题,函数的性质及应用
分析:(1)将函数f(x)写成分段函数的形式,再画出图象,注意各段的范围;
(2)由图象写出单调区间,注意多个增区间或减区间之间,不能用并集;
(3)根据图象只要比较f(-3)和f(
)的大小,即可得到最值.
(2)由图象写出单调区间,注意多个增区间或减区间之间,不能用并集;
(3)根据图象只要比较f(-3)和f(
| 3 |
| 2 |
解答:
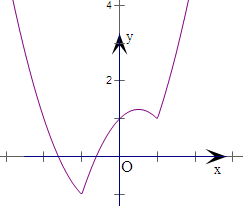 解:(1)函数f(x)=|x2-1|+x=
解:(1)函数f(x)=|x2-1|+x=
,
画出图象如右.
(2)由图象可知函数f(x)的单调增区间为(-1,
),(1,+∞)
单调减区间为(-∞,-1),(
,1);
(3)当x∈[-3,
]时,由于f(-3)=8-3=5,f(
)=
,
f(-1)=-1.
则函数y=f(x)的最大值为5,最小值为-1.
 解:(1)函数f(x)=|x2-1|+x=
解:(1)函数f(x)=|x2-1|+x=
|
画出图象如右.
(2)由图象可知函数f(x)的单调增区间为(-1,
| 1 |
| 2 |
单调减区间为(-∞,-1),(
| 1 |
| 2 |
(3)当x∈[-3,
| 3 |
| 2 |
| 3 |
| 2 |
| 11 |
| 4 |
f(-1)=-1.
则函数y=f(x)的最大值为5,最小值为-1.
点评:本题考查含绝对值的函数的图象和性质,注意单调区间有多个时,不能运用并集,属于基础题和易错题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
函数f(x)=-x3-2x2+4x,当x∈[-3,3]时,有f(x)≥m2-14m恒成立,则实数m的取值范围是( )
| A、(-3,11) |
| B、(3,11) |
| C、[3,11] |
| D、[2,7] |
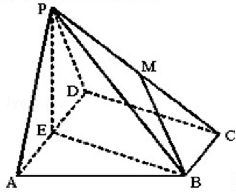 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD中点,M是棱PC的中点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD中点,M是棱PC的中点,PA=PD=2,BC=