题目内容
已知函数f（x）=
-4，求证：函数f（x）在（0，+∞）上是减函数．
| 3 |
| x |
考点：函数单调性的判断与证明
专题：计算题,证明题,函数的性质及应用
分析：用定义法证明单调性一般可以分为五步，取值，作差，化简变形，判号，下结论．
解答：
证明：任取x1，x2∈（0，+∞），且x1＜x2，则
f（x1）-f（x2）=
-4-（
-4）
=
，
∵0＜x1＜x2，
∴x2-x1＞0，x1x2＞0；
则f（x1）-f（x2）＞0，
则函数f（x）在（0，+∞）上是减函数．
f（x1）-f（x2）=
| 3 |
| x1 |
| 3 |
| x2 |
=
| 3(x2-x1) |
| x1x2 |
∵0＜x1＜x2，
∴x2-x1＞0，x1x2＞0；
则f（x1）-f（x2）＞0，
则函数f（x）在（0，+∞）上是减函数．
点评：本题考查了函数单调性的证明，一般有两种方法，定义法，导数法．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
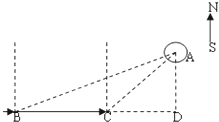海中一小岛，周围3.8mile内有暗礁，海轮由西向东航行，望见这岛在北偏东80°，航行8n mile以后，望见这岛在北偏东60°，如查这艘海轮不改变航行继续前进，有没有触礁的危险．（精确到0.001，cos10°=0.9848）已知f（x）是定义在实数集R上的奇函数，且f（x+4）=f（x） 当x∈（0，2）时，f（x）=2x2，则f（2011）=（ ）
| A、98 | B、-98 | C、2 | D、-2 |
设Sn是等差数列{an}的前n项和，若
=1，则
=（ ）
| S9 |
| S5 |
| a5 |
| a3 |
A、
| ||
B、
| ||
C、
| ||
D、
|