Question

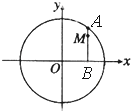如图，设A是圆x²+y²=6上的动点，点B是A在x轴上投影，M为AB上一点，且|MB|=

3

3

|AB|．当A在圆上运动时，点M的轨迹为曲线G．过点（m，0）（m＞

6

）且倾斜角为

5π

6

的直线l交曲线G于C，D两点．
（1）求曲线G的方程；
（2）若点F是曲线G的右焦点且∠CFD∈[

π

3

，

π

2

]，求m的取值范围．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设点M的坐标是（x，y），A（x_A，x_B），由已知得x_A=x，且yA=

3

y，由此能求出G的方程．
（2）直线l交曲线G于C，D两点，且∠CFD∈[

π

3

，

π

2

]．由题意得直线l的方程为y=-

3

3

(x-m)．（m＞

6

）．由

x2 6 + y2 2 =1 y=- 3 3 (x-m)

，得2x²-2mx+m²-6=0．由此利用根的判别式、韦达定理，结合已知条件能求出m的取值范围．

解答： 解：（1）设点M的坐标是（x，y），A（x_A，x_B），
因为点B是A在x轴上投影，M为AB上一点，
且|MB|=

3

3

|AB|，所以x_A=x，且yA=

3

y，
∵A在圆x²+y²=6上，∴x2+(

3

y)2=6，
整理得

x2

6

+

y2

2

=1．即G的方程是

x2

6

+

y2

2

=1．
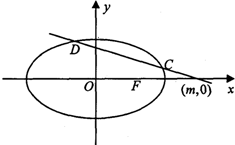
（2）如下图，直线l交曲线G于C，D两点，
且∠CFD∈[

π

3

，

π

2

]．
由题意得直线l的方程为y=-

3

3

(x-m)．（m＞

6

）．
由

x2 6 + y2 2 =1 y=- 3 3 (x-m)

，消去y，得2x²-2mx+m²-6=0．
由△=4m²-8（m²-6）＞0，解得-2

3

＜m＜2

3

．
又m＞

6

，∴

6

＜m＜2

3

．
设C（x₁，y₁），D（x₂，y₂），则x₁+x₂=m，x1x2=

m2-6

2

，
∴y1y2=[-

3

3

(x1-m)]•[-

3

3

(x2-m)]=

1

3

x1x2-

m

3

(x1+x2)+

m2

3

．
∵

FC

=（x₁-2，y₁），

FD

=（x₂-2，y₂）．
∴

FC

•

FD

=（x₁-2）（x₂-2）+y₁y₂
=

4

3

x1x2-

m+6

3

(x1+x2)+

m2

3

+4
=

2(m2-3m)

3

．
又由椭圆方程，知y2=

6-x2

3

，
∵|

FC

|=

(x1-2)2+y12

=

(x12-4x1+4)+ 6-x12 3

=

2 3 (x1-3)2

=

2 3

(3-x1)，
|

FD

|=

(x2-2)2+y22

=

(x22-4x2+4)+ 6-x22 3

=

2 3 (x2-3)2

=

2 3 (3-x2)

，
∴|

FC

||

FD

|=

2

3

(3-x1)(3-x2)=

2

3

[x₁x₂-3（x₁+x₂）+9]
=

1

3

(m2-6m+12)，
∴cos∠CFD=

FC • FD

| FC |•| FD |

=

2 3 (m2-3m)

1 3 (m2-6m+12)

=

2(m2-3m)

m2-6m+12

．
∵∠CFD∈[

π

3

，

π

2

]，∴cos∠CFD∈[0，

1

2

]．
∴0≤

2(m2-3m)

m2-6m+12

≤

1

2

，
∴

2(m2-3m)≥0 m2-2m-4≤0

，∴

m≤0或m≥3 1- 5 ≤m≤1+ 5

，
故1-

5

≤m≤0或3≤m≤1+

5

，
又

6

＜m＜2

3

，故3≤m≤1+

5

．

点评：本题考查曲线方程的求法，考查满足条件的实数的取值范围的求法，解题时要认真审题，注意函数与方程思想的合理运用．