题目内容
 如图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若
如图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若| AB |
| AM |
| AC |
| AN |
| A、1 | ||
| B、2 | ||
| C、-2 | ||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据平面内三点共线的充要条件进行判断,即若A,B,C三点共线,则
=x
+y
,(x+y=1).
| OC |
| OA |
| OB |
解答:
解:由已知得
=
(
+
),
结合
=m
,
=n
,所以
=
m
+
n
.
又因为O,M,N三点共线,所以
m+
n=1,
所以m+n=2.
故选B
| AO |
| 1 |
| 2 |
| AB |
| AC |
结合
| AB |
| AM |
| AC |
| AN |
| AO |
| 1 |
| 2 |
| AM |
| 1 |
| 2 |
| AN |
又因为O,M,N三点共线,所以
| 1 |
| 2 |
| 1 |
| 2 |
所以m+n=2.
故选B
点评:本题考查了平面内三点共线的充要条件的推论.注意抓住是从同一点出发的三个向量间的关系,注意辨析.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
直线l过点A(3,1)与x轴正向、y轴正向分别交于M、N两点,则|MA|•|NA|的最小值为( )
| A、2 | B、4 | C、6 | D、8 |
在正方体ABCD-A1B1C1D1中,下列四队截面中彼此平行的一对是( )
| A、A1BC1与ACD1 |
| B、B1CD1与BDC1 |
| C、B1D1D与BDA1 |
| D、A1DC1与AD1C |
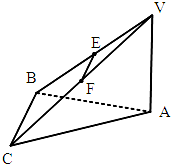 如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.
如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.