题目内容
直线l过点A（3，1）与x轴正向、y轴正向分别交于M、N两点，则|MA|•|NA|的最小值为（ ）
| A、2 | B、4 | C、6 | D、8 |
考点：直线的截距式方程
专题：直线与圆
分析：过M分别作x轴、y轴的垂线，垂足分别为P、N，设∠MAP=α，建立三角函数关系即可得到结论．
解答：
解：过M分别作x轴、y轴的垂线，垂足分别为P、N
设∠MAP=α，则Rt△MPA中，
sinα=
，得|MA|=
，
同理可得：|MB|=
∴|MA|•|MB|=
•
=
∵sin2α∈（0，1]，
∴当2α=90°时，即α=45°时，sin2α=1达到最大值，|MA|•|MB|=
=6达到最小值，
故选：C
设∠MAP=α，则Rt△MPA中，
sinα=
| |MP| |
| |MA| |
| 1 |
| sinα |
同理可得：|MB|=
| 3 |
| cosα |
∴|MA|•|MB|=
| 1 |
| sinα |
| 3 |
| cosα |
| 6 |
| sin2α |
∵sin2α∈（0，1]，
∴当2α=90°时，即α=45°时，sin2α=1达到最大值，|MA|•|MB|=
| 6 |
| sin2α |
故选：C
点评：本题给出经过定点的直线，求满足特殊条件的直线方程．着重考查了直线的基本量与基本形式、基本不等式求最值和解直角三角形等知识，属于中档题．
练习册系列答案
相关题目
甲、乙两人在一次赛跑中路程s与t的函数关系如图所示，则下列说法正确的是（ ）
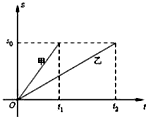
| A、甲比乙先出去 |
| B、乙比甲跑的路程多 |
| C、甲先到达终点 |
| D、甲、乙两人的速度相同 |
已知方程x2+x+m=0（m∈R）有两个虚根α，β，若|α-β|=3，则m的值是（ ）
A、-2或
| ||
| B、-2 | ||
C、
| ||
D、-
|
由不大于7的质数组成的集合是（ ）
| A、﹛1，2，3，5，7﹜ |
| B、﹛2，3，5，7﹜ |
| C、﹛2，3，5﹜ |
| D、﹛x|x≤7﹜ |
如图，在△ABC中，点O是BC的中点．过点O的直线分别交直线AB，AC于不同的两点M，N，若