题目内容

3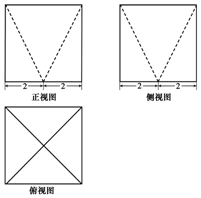．某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直，则该几何体的表面积是（　　）
A．$96+16\sqrt{5}$B．$80+16\sqrt{5}$C．$80+32\sqrt{5}$D．$96+32\sqrt{5}$

分析 通过三视图可知该几何体是一个正方体扣去一个正四棱锥，计算五个正方形的面积与四个等腰三角形的面积即可．

解答 解：由三视图可知该几何体是一个正方体扣去一个正四棱锥，如图．
则正四棱锥的侧面是底为4、高为$\sqrt{{2}^{2}+{4}^{2}}$=$2\sqrt{5}$的等腰三角形，
其面积S1=$\frac{1}{2}$×4×$2\sqrt{5}$=$4\sqrt{5}$，
所以该几何体的面积为5×4×4+4×S1=80+16$\sqrt{5}$，
故选：B．

点评 本题考查由三视图求表面积，考查空间想象能力，考查三角形面积公式，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
8．（1）从1，2，3，4四个数字中任取两个数字组成两位数，共有多少个不同的两位数？
（2）由1，2，3，4四个数字共能组成多少个没有重复数字的四位数？
14．（x-$\frac{1}{2x}$）8的展开式中常数为（　　）
A．$\frac{1}{2}$B．$\frac{35}{8}$C．$\frac{3}{2}$D．-$\frac{3}{2}$
11．已知空间三点A（0，2，3），B（-2，1，6），C（1，-1，5）．
（1）求cos＜$\overrightarrow{AB}，\overrightarrow{AC}$＞；
（2）求以AB，AC为边的平行四边形的面积．
18．已知x∈（0，+∞），观察下列各式：$x+\frac{1}{x}＞2，x+\frac{4}{x^2}=\frac{x}{2}+\frac{x}{2}+\frac{4}{x^2}≥3，x+\frac{27}{x^3}=\frac{x}{3}+\frac{x}{3}+\frac{27}{x^3}≥4，…$类比得$x+\frac{a}{x^n}≥n+1（{n∈{N^*}}）$，则a=nn．
8．已知函数f（x）=log${\;}_{\frac{1}{e}}}$（x2+$\frac{1}{e}$）-|${\frac{x}{e}}$|，则使得f（x+1）＜f（2x-1）成立x的范围是（0，2）．
15．已知集合M={（x，y）|y=f（x）}，若对于任意实数对（x1，y1）∈M，存在（x2，y2）∈M，使x1x2+y1y2=0成立，则称集合M具有∟性，给出下列四个集合：
①M={（x，y）|y=x3-2x2+3}；      ②M={（x，y）|y=log2（2-x）}；
③M={（x，y）|y=2-2x}；          ④M={（x，y）|y=1-sinx}；
其中具有∟性的集合的个数是（　　）
A．1B．2C．3D．4
12．2015年9月3日，抗战胜利70周年纪念活动在北京隆重举行，收到全国人民的瞩目．纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等，据统计，抗战老兵由于身体原因，参加纪念大会、阅兵式、招待会这三个环节（可参加多个，也可都不参加）的情况及其概率如表所示：
参加纪念活动的环节数0123
概率$\frac{1}{6}$mn$\frac{1}{3}$
（1）若m=2n，则从这60名抗战老兵中按照参加纪念活动的环节数分层抽取6人进行座谈，求参加纪念活动环节数为1的抗战老兵中抽取的人数；
（2）某医疗部门决定从（1）中抽取的6名抗战老兵中随机抽取2名进行体检，求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率．
13．由y=（x-2）2与y=4x-8所围图形的面积为（　　）
A．6B．$\frac{54}{3}$C．$\frac{32}{3}$D．9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网